Chip Placement with Deep Reinforcement Learning

Written by Kyeongmin Woo on 15 Feb 2021

Chip Placement 문제는 반도체 설계 공정 중 하나로 조합 최적화 문제입니다. 이번 포스팅에서는 Chip Placement 문제에 강화학습을 적용한 Google의 Chip Placement with Deep Reinforcement Learning[1] 논문(이하 Google의 Chip Placement 논문)을 소개해보고자 합니다.

구글은 어떤 문제를 풀었나?

현재 범용적으로 사용되고 있는 CPU, GPU, DRAM과 같은 반도체들은 수없이 많은 소자들로 구성되어 있고, 각각의 소자들은 기능에 맞게 연결되어 있습니다. 새로운 건물을 짓는 것과 마찬가지로 반도체 생산 또한 설계부터 제조까지 일련의 공정들을 따라 진행되는데, 나노미터 단위의 소자들을 다루어야 하다보니 각각의 공정들은 매우 높은 복잡도를 가지고 있습니다. Chip Placement 문제는 반도체 설계 및 제조의 여러 공정 중에서도 Placement & Routing(P&R) 공정에 속하는 문제로, 단순하게 말하면 주어진 공간 상에 논리적으로 정의된 반도체의 소자들을 배치하는 작업이라고 할 수 있습니다.

P&R 공정은 논리적으로 정의되어 있는 반도체 설계 도면을 실제 물리적인 공간 상에 어떻게 구현할지 결정하는 단계입니다. 따라서 P&R 공정의 입력은 반도체의 논리적인 설계도가 되고, 출력은 각각의 소자 및 이들을 연결하는 선들의 위치가 정확하게 정해져 있는 물리적인 설계도가 됩니다.

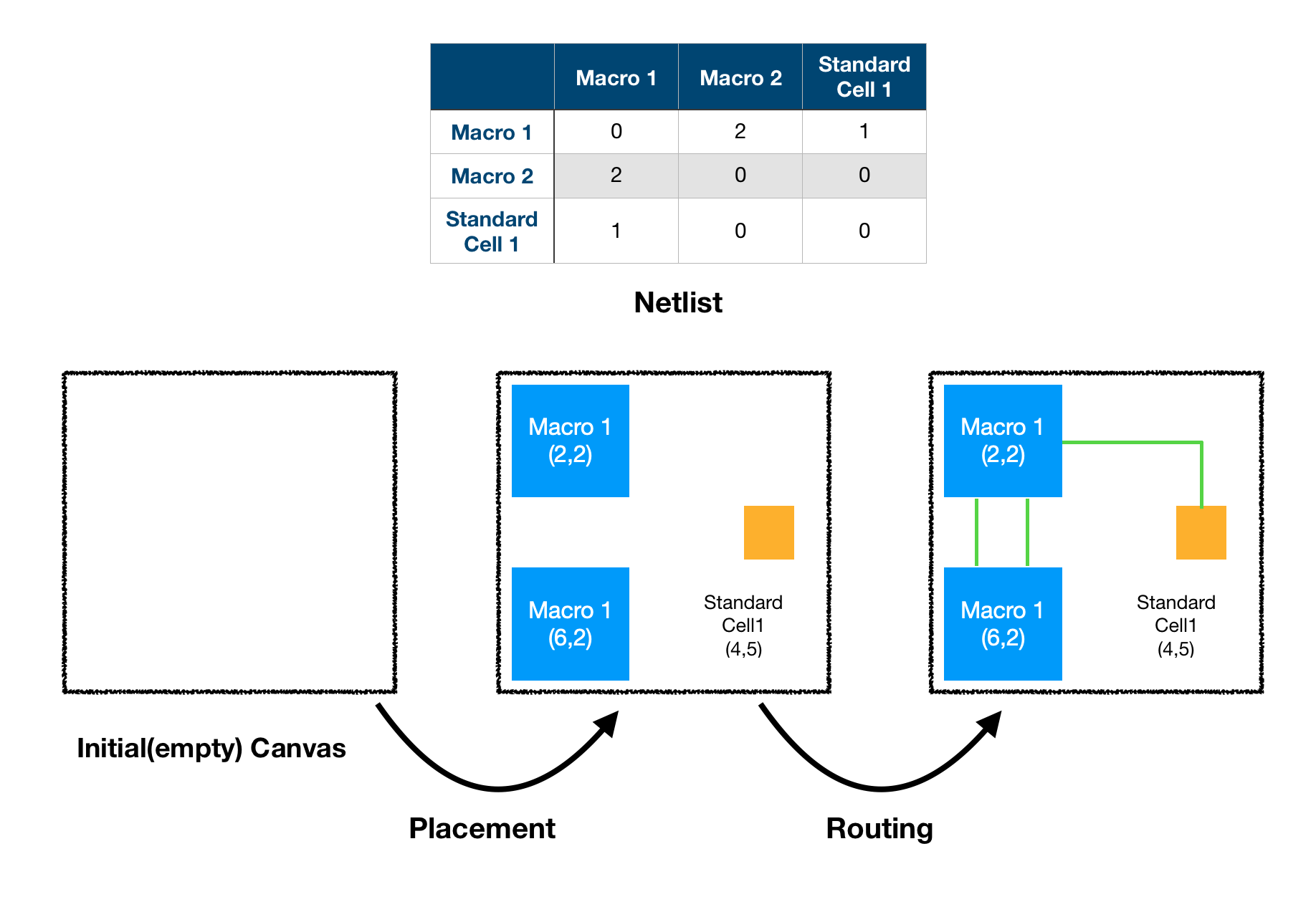
normal gradient — [그림1] - Placement & Routing

문제에 대한 정확한 이해를 위해 산업에서 사용되는 용어들을 먼저 정리하고 넘어가도록 하겠습니다. 앞서 P&R 공정의 입력을 반도체의 논리적인 설계도라고 하였는데, 여기서 말하는 논리적 설계도란 각 소자들의 특성과 연결 관계를 논리적으로 정의하고 있는 데이터이며 이를 Netlist라고 합니다. 그리고 이 Netlist를 구성하는 소자들 중에서 상대적으로 크기가 큰 소자들을 Macro, 작은 소자들을 Standard Cell이라고 합니다. 각각의 소자들의 연결로서, 전기적 신호를 주고 받는 데에 사용되는 선은 Wire라고 부릅니다. 마지막으로 Macro, Standard Cell, Wire 등 반도체를 구성하는 모든 것이 배치되는 공간을 Chip Canvas라고 합니다.

좋은 배치란 무엇일까?

그렇다면 Chip Canvas 상에 소자들을 어떻게 배치해야 잘 배치했다고 할 수 있을까요. 산업에서는 Performance, Power, Area, 줄여서 PPA라고 부르는 기준들을 주로 사용합니다. 쉽게 말해 Clock Frequency(Performance)가 높고, 전력(Power)을 적게 소모하며, 사용하는 Chip Canvas의 크기(Area)가 작을수록 좋은 배치라는 것입니다. 이를 반대로 생각해보면 각각의 소자들을 어떻게 배치하느냐에 따라 반도체의 수준이 결정된다고 할 수 있습니다.

소자의 배치와 PPA의 인과 관계를 생각해 본다면 세 가지 기준 중 Area를 가장 쉽게 이해할 수 있습니다. 소자들 간의 빈 공간이 없도록 배치한다면 필요한 배치 영역의 크기가 작을 것이고, 빈 공간이 많아지면 많아질수록 커질 것입니다. Area가 작아지게 되면 하나의 웨이퍼(Wafer)[8]에 많은 Chip을 생산할 수 있다는 것을 의미하므로 설계 효율이 높아지게 됩니다.

또한 Wire의 길이가 짧으면 짧을수록 전기 신호가 더욱 빨리 도달할 수 있어 높은 Clock Frequency가 가능해지고, 동시에 Wire를 통과하며 사용하는 전력이 줄어들게 됩니다. 이는 짧은 거리로 갈 때 더 빨리 도착하고 동시에 더 적은 연료를 소모하는 것과 비슷합니다.

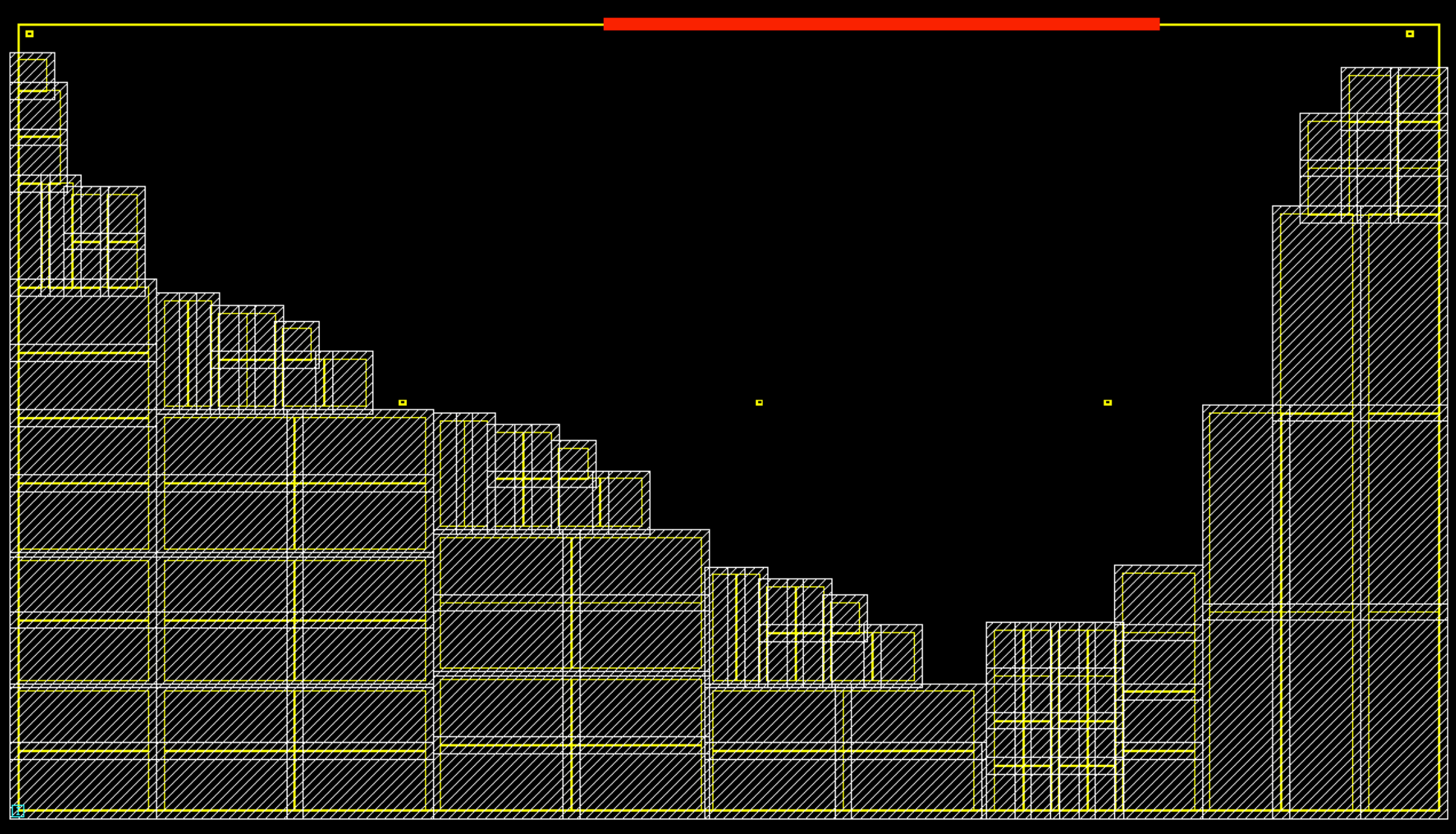
위의 세 가지 기준만 놓고 본다면 소자들 간의 연결성에 비례하여 가깝게 배치하면 최적 배치를 달성할 수 있을 것으로 보입니다. 전체적으로 필요한 면적이나, Wire의 길이 모두 서로 연결된 소자들이 가까우면 줄어들 것이기 때문입니다. 하지만 연결성 만을 고려해서는 현실적인 배치가 이뤄질 수가 없는데, Chip Canvas의 영역마다 Routing Resource, 즉 할당 가능한 Wire의 수가 한정적이기 때문입니다.

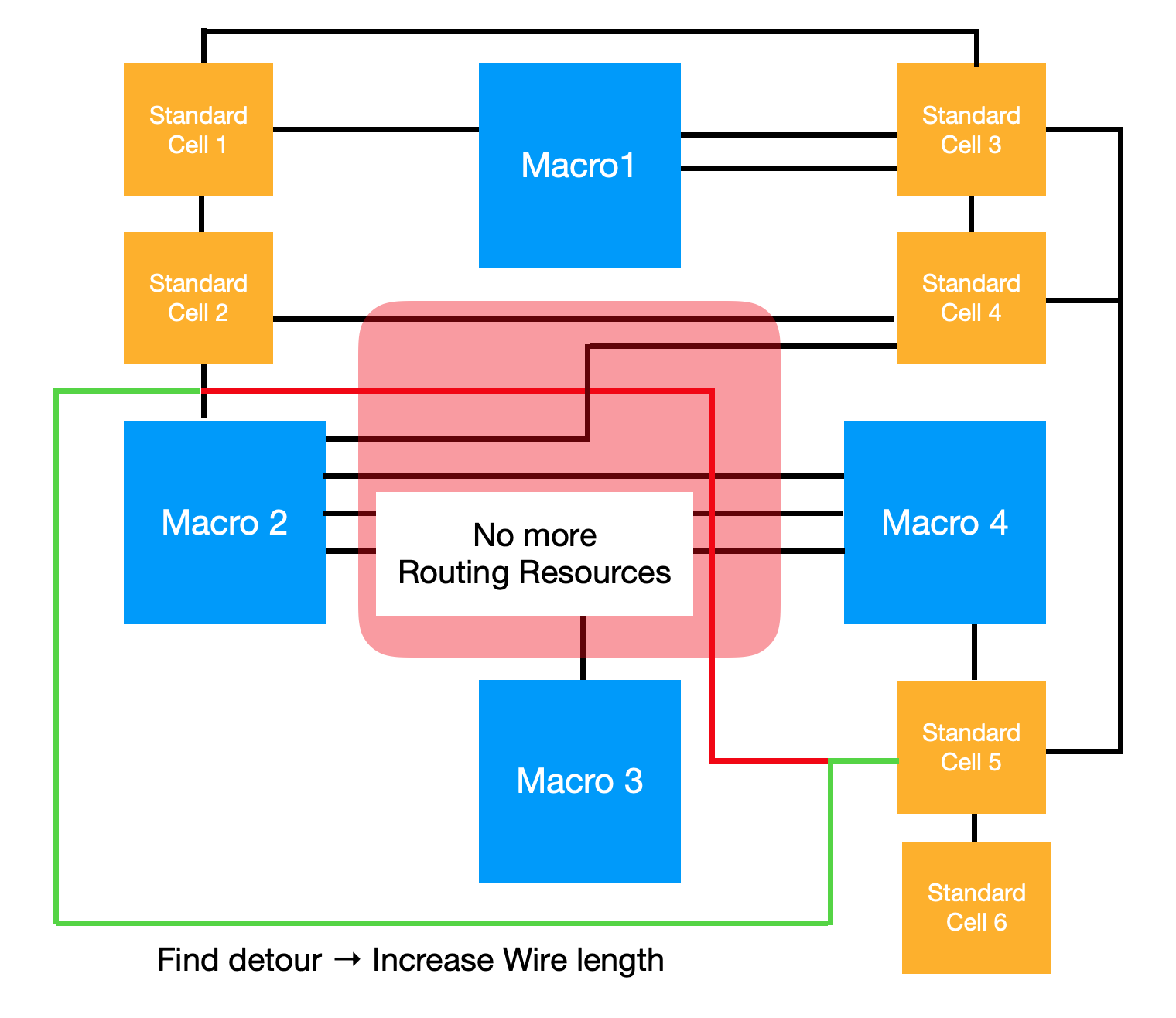
위의 그림에서 빨간 선은 Macro2와 Standard Cell 5를 연결하는 가장 짧은 경로를 나타냅니다. 그런데 빨간 선이 통과하는 구간에 이미 너무 많은 Wire가 배치되어 있어 더 이상 Routing Resource가 존재하지 않는 상황입니다. 이러한 경우에는 녹색 선과 같이 우회하여 Wire를 배치하게 되고, 전체적인 Wire Length가 길어집니다.

기존에는 어떻게 풀었을까?

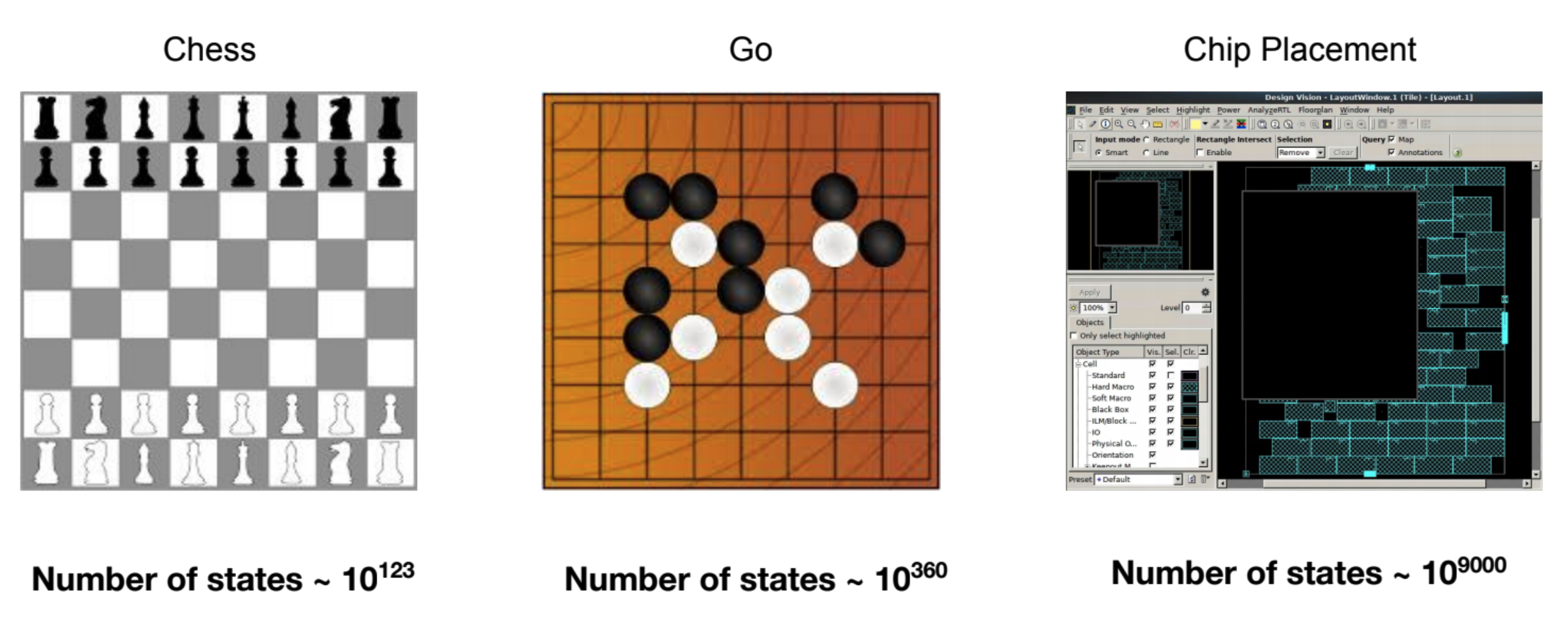
위와 같은 여러가지 현실적인 제약 조건들까지 만족하며 배치해야 한다는 점에서 Chip Placement 문제의 복잡도는 매우 높다고 할 수 있습니다. 체스, 바둑과 같이 기존에 강화학습 알고리즘으로 해결한 다른 문제들과 비교해 볼 때 경우의 수만 보더라도 Chip Placement 문제가 훨씬 복잡합니다[9].

그런데 Chip Placement 문제에 대해서도 최적의 해를 찾는 것은 어렵지만 그에 가까운 해를 찾는 휴리스틱 알고리즘들은 많이 알려져 있습니다. Simulated Annealing과 Force-Directed Method가 대표적이며[4], 현재 반도체 산업에서는 이러한 알고리즘들을 다양하게 변형하여 여러 상황에서 최적의 P&R을 찾는 시도를 하고 있습니다. 기존 알고리즘에 대한 구체적인 설명은 VLSI Cell Placement Techniques[4]에서 자세히 다루고 있는 만큼 참고하시면 좋을 것 같습니다.

Five major algorithms for placement are discussed: simulated annealing, force-directed placement, rein-cut placement, placement by numerical optimization, and evolution-based placement. (VLSI Cell Placement Techniques)

이와 관련하여 산업의 이야기를 덧붙이면 P&R 뿐만 아니라 반도체의 설계 과정에서 많은 부분을 자동화해주는 툴을 EDA(Electronic Design Automation)라고 하고, 많은 반도체 설계 전문 회사들이 Cadence, Synopsys와 같은 글로벌 기업의 EDA Tool을 사용하여 설계 과정 상의 여러 복잡한 문제들을 해결하고 있습니다. 하지만 자동화 툴이라고 해서 모든 것이 100% 자동적으로 이뤄지는 것은 아니며, EDA Tool을 누가 어떻게 사용하느냐에 따라 결과물의 수준이 확연히 달라집니다. P&R 문제만 놓고 보더라도 크기가 상대적으로 크고, 내부의 구조가 미리 결정되어 있는 Hard Macro의 경우에는 전문가가 직접 배치하는 것이 일반적입니다.

배치 문제에 강화학습 적용하기

Google의 Chip Placement 논문에서 제시하는 방법은 전문가가 직접 배치하고 있는 Hard Macro들만 강화학습 에이전트로 배치하고 있습니다. 즉 전체 Chip Placement 문제를 강화학습 알고리즘으로 해결하는 것이 아니며, 정확하게 말하면 수백 수천만 개의 소자들 중에서 몇백 개의 Macro만 강화학습으로 배치합니다(Few hundred macros and millions of standard cells).

에이전트가 배치하지 않는 다른 모든 소자들에 대해서는 전통적인 Chip Placement 방법론 중 하나인 Force-Directed Method를 사용합니다. 이때 전통적인 알고리즘을 사용한다 하더라도 배치 대상의 개수가 너무 많기 때문에 Standard Cell은 연결성이 높은 소자들끼리 Clustering을 진행한 후, Cluster 단위로 배치를 수행합니다. 이를 통해 배치 대상의 개수를 수백만 개에서 수천 개 수준으로 축소하여 복잡성을 낮추고 있습니다.

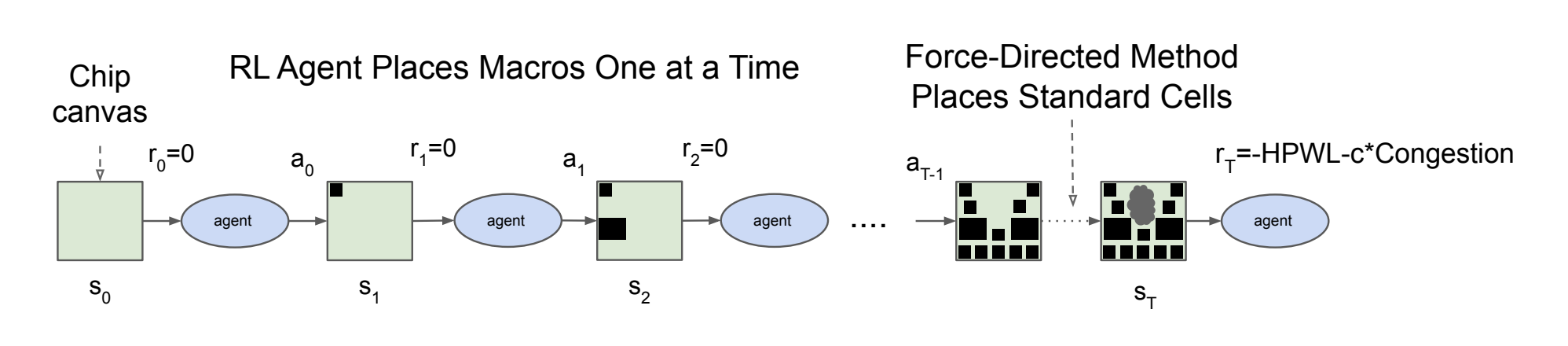
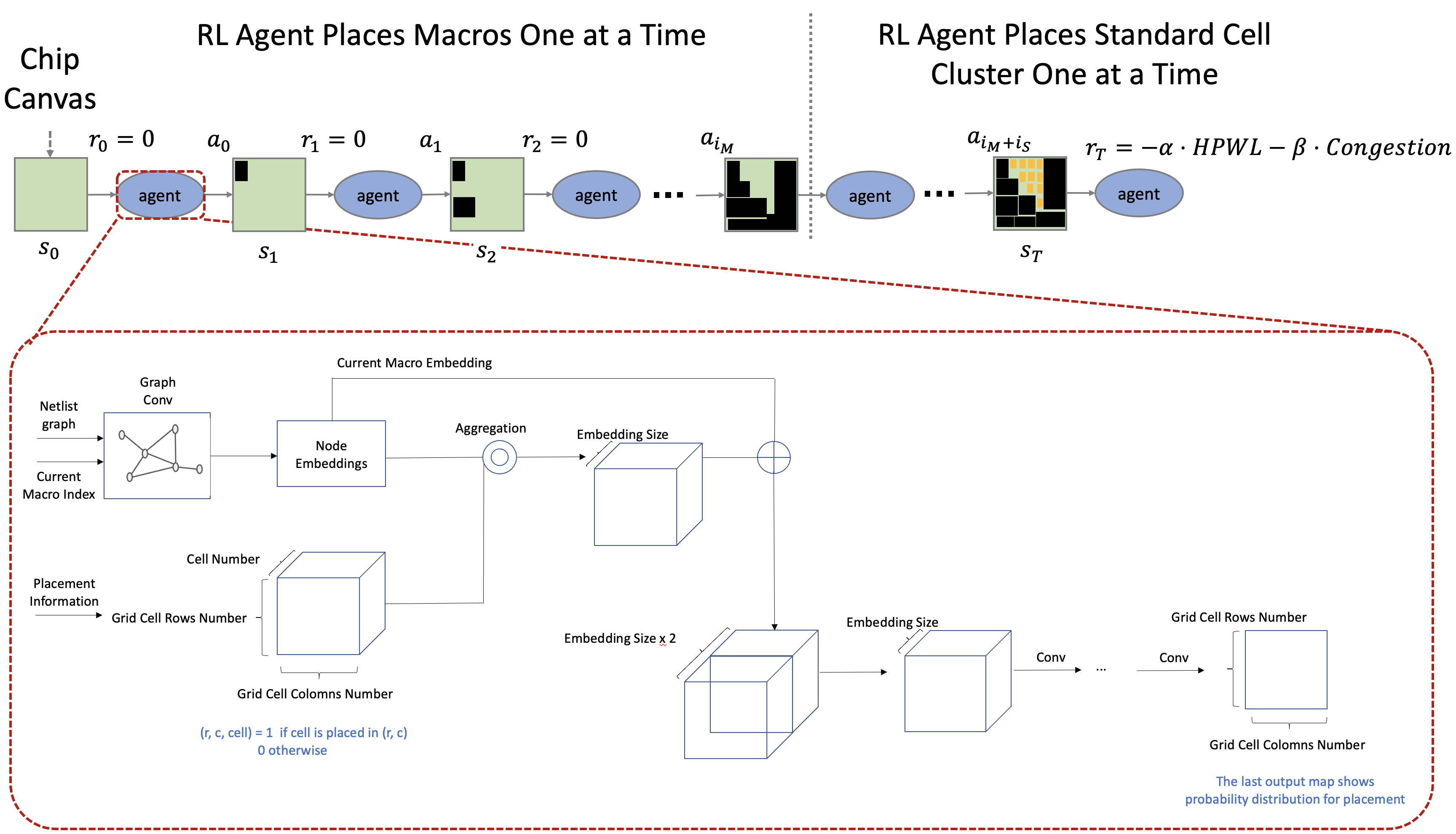
위 그림[1]은 Google Chip Placement 논문의 배치 순서를 나타내고 있습니다. 검은 박스로 나타낸 것이 Hard Macro, 회색 구름으로 나타낸 것이 Standard Cell Cluster 입니다.

배치 문제를 강화학습에 맞게 정의하기

어떤 문제를 강화학습으로 풀기 위해서는 주어진 문제를 MDP(Markov Decision Process)로 정의해야 합니다. 참고로 MDP는 강화학습의 기본적인 가정으로서, 확률적인 환경 속에서 이산 시간마다 의사결정(Discrete-time stochastic control)을 내려야 하는 상황을 모델링하는 방법입니다[5].

Chip Placement 문제를 MDP로 정의한다는 것은 구체적으로 MDP의 네 가지 요소인 \((S, A, P_{s,s'}, R)\)을 문제의 특성에 맞게 정의한다는 것입니다. 논문에서는 각각에 대해 다음과 같이 정의하고 있습니다.

\(S\): State Space

State는 현재 에이전트가 처해 있는 상황에 대한 정보를 의미합니다. Chip Placement 문제의 특성상 여기에는 여러 정보들이 포함될 수 있는데, 논문에서 제안하는 정보들은 다음과 같습니다.

소자들 간의 연결성에 대한 정보
Chip Canvas의 상태, 즉 어떤 Macro가 어디에 배치되어 있는지에 대한 정보
이번 Step에 배치될 Macro에 대한 정보(크기 등)
Macro를 배치 할 수 있는 영역에 관한 정보

\(A\): Action Space

Chip Placement 문제인 만큼 에이전트의 Action은 Macro의 배치 위치로 정의합니다. Chip Canvas를 여러 개의 Grid 영역으로 나누고 그 중 Macro를 배치할 영역을 하나 선택하는 방식으로 이뤄지기 떄문에 Action의 가짓수는 Grid의 크기(\(\text{row} \times \text{col}\))가 됩니다.

\(P(s' \vert s, a)\): State Transition

State Transition이란 State \(s\)에서 Action \(a\)를 선택했을 때, 그 결과로 다음 State는 무엇이 될 것인지를 의미합니다. State를 구성하는 여러 정보 중 이미 배치된 Macro의 위치나, 특정 영역에 배치 가능한지에 대한 정보들은 에이전트가 선택한 Action에 따라 결정되는 반면 배치의 순서나, Netlist의 특성 등은 환경의 내부 로직에 따라 결정됩니다.

\(R\): Reward Function

State Transition이 현재 State와 Action의 조합의 결과로 다음에 주어질 State에 관한 것이라면, Reward는 현재 State와 Action의 조합이 얼마나 좋은지 평가하는 스칼라 값입니다. 강화학습은 Reward의 총합에 대한 기댓값을 높이는 방향으로 업데이트 되기 때문에 Reward를 결정하는 함수가 어떻게 되어있느냐에 따라 강화학습 알고리즘의 학습 방향이 결정됩니다. 가능한 모든 Netlist Graph 집합을 \(G\)(크기 \(K\))라고 하고, 각 Netlist \(g\)에 대한 배치 결과를 \(p\)라고 할 때 목적 함수 \(J\)는 다음과 같이 정의합니다.

\[J(\theta, G) = {1 \over K} \Sigma_{g \backsim G} E_{g,p \backsim \pi_\theta} [R_{p,g}]\]

Chip Placement 문제를 해결하는 에이전트를 만들기 위해서는 이상적으로 생각하는 배치에 대해서는 높은 Reward를, 그렇지 않은 배치에 대해서는 낮은 Reward를 주어야 합니다. 이를 가장 정확하게 반영하는 메트릭은 앞서 소개한 PPA의 측정 값인 WNS, Dynamic Power 등의 값을 그대로 넣어주는 것입니다.

WNS는 Worst Negative Setup-time Slack의 약자로, 쉽게 말해 현재 배치가 특정 Clock Frequency를 유지할 수 있는지를 나타내는 척도라고 할 수 있습니다. 이 값이 음수이면 사용이 불가능한 배치임을 뜻합니다. Dynamic Power는 FPGA 보드의 구동에 소요되는 전력을 제외하고 특정 배치를 유지하는 데에 소요되는 전력을 의미합니다.

하지만 여기에 한 가지 문제가 있다면 어떤 배치에 대해 정확한 WNS와 Dynamic Power를 계산하기 위해서는 Placement 이후 작업인 Routing이 완료되어야 한다는 점입니다. 이렇게 되면 한 번의 Reward 계산에 매우 많은 시간이 요구됩니다. 학습을 위해 많은 Transition \((s, a, r, s')\)을 요구하는 강화학습의 특성상 Reward 계산에 너무 많은 시간이 들어가게 되면 전체적인 학습 속도가 크게 느려질 수밖에 없습니다.

Wire Length & Routing Congestion

이러한 문제를 해결하기 위해 논문에서는 연산 속도가 빠르면서도 전력 소모 및 성능을 간접적으로 파악할 수 있는 값들인 Wire Length와 Routing Congestion을 Reward 계산에 사용합니다. Wire는 전기 신호가 통과해야 하는 통로이므로 그 길이가 짧을수록 더욱 빠르고 적은 전력으로 신호가 전달됩니다. 이러한 점에서 Wire Length가 짧으면 Clock Frequency(Performance)와 Power의 측면에서 이점이 있고, 따라서 Wire Length의 길이에 따라 패널티를 부여하고 있습니다.

그런데 여기서 말하는 Wire Legnth란 단순히 소자 간 물리적인 거리만을 고려하여 계산된 값입니다. 앞서 확인한 대로 실제 Chip Canvas에서는 특정 영역에 Wire가 밀집하면 몇몇 Wire는 우회하여 배치해야 하고, 정확한 Reward 계산을 위해서는 이러한 특성이 반영되어야 합니다. 두 번째 항에서 영역별 Wire의 밀집도라고 할 수 있는 Routing Congestion를 계산하여 패널티를 부여하는 것은 이를 반영한 것입니다.

\[R_{p,q} = -\text{Wirelength}(p, g) - \lambda \text{Congestion}(p, g) \\ \text{S.t. } \text{density}(p,g) \leq \text{max}_\text{density}\]

위와 같이 Reward를 계산하는 것은 정확도를 다소 희생하되, 연산에 필요한 비용과 시간을 줄인 것으로 볼 수 있습니다. 참고로 Reward는 모든 Macro와 Standard Cell이 배치된 이후에 한 번만 계산합니다. 그 이외의 경우에는 Reward가 항상 0으로 저장됩니다. 논문에서는 위의 식과 관련하여 \(\lambda = 0.01\), \(\max_{\text{density}} = 0.6\)으로 hyper parameter를 설정하여 실험을 진행했다고 합니다.

(1) Wire Length

Wire Length를 계산하는 방법으로는 Half-Perimenter Wire Length(HPWL)을 사용합니다. 하나의 Wire마다 계산이 이뤄지는 HPWL은 Wire에 연결되어 있는 모든 소자들을 포함하는 경계 상자를 먼저 그린 후 상자 둘레의 절반을 Wire의 길이로 추정하는 방법입니다. 수식[1]으로 표현하면 어떤 Wire \(i\)의 길이는 다음과 같이 계산됩니다.

\[\eqalign{ \text{HPWL}(i) = &(\max_{b \in i}\{ x_b \} - \min_{b \in i} \{ x_b \} + 1)\\ +& (\max_{b \in i}\{ y_b \} - \min_{b \in i} \{ y_b \} + 1) }\]

(2) Routing Congestion

Chip Canvas는 영역 별로 일정한 Routing Resoure를 가지고 있으며, 이를 모두 사용하게 되면 해당 영역으로는 더 이상 새로운 Wire를 할당할 수 없습니다. 이러한 점 때문에 각 소자를 연결하는 Wire가 특정 영역에 집중되는 경우 실제 Wire의 길이가 크게 늘어날 가능성이 있고, 그 결과 반도체의 전체 성능 또한 나빠지게 됩니다.

이러한 문제를 피하려면 특정 영역에 너무 많은 Wire가 할당되는 상황을 피해야 하는데, 논문에서는 Routing Congestion, 즉 영역 별로 할당된 Wire들의 집중도가 높으면 Reward에 Penalty를 주는 방식을 사용하고 있습니다.

(3) Placement Density

위의 Reward 계산식에서는 Placement Density를 Hard Constraint로 두고 있습니다. Placement Density란 배치된 소자들의 밀집도를 말하는데, 밀집도가 일정 수준(\(0.6\)) 이상으로 높아지면 Wire Length가 지나치게 커지는 경향이 있다고 합니다. 즉 현실적인 배치 중에서 학습이 이뤄지도록 Domain Knowledge에 따라 Search Space를 줄여주는 제약식이라고 할 수 있습니다.

배치 문제를 위한 강화학습 모델

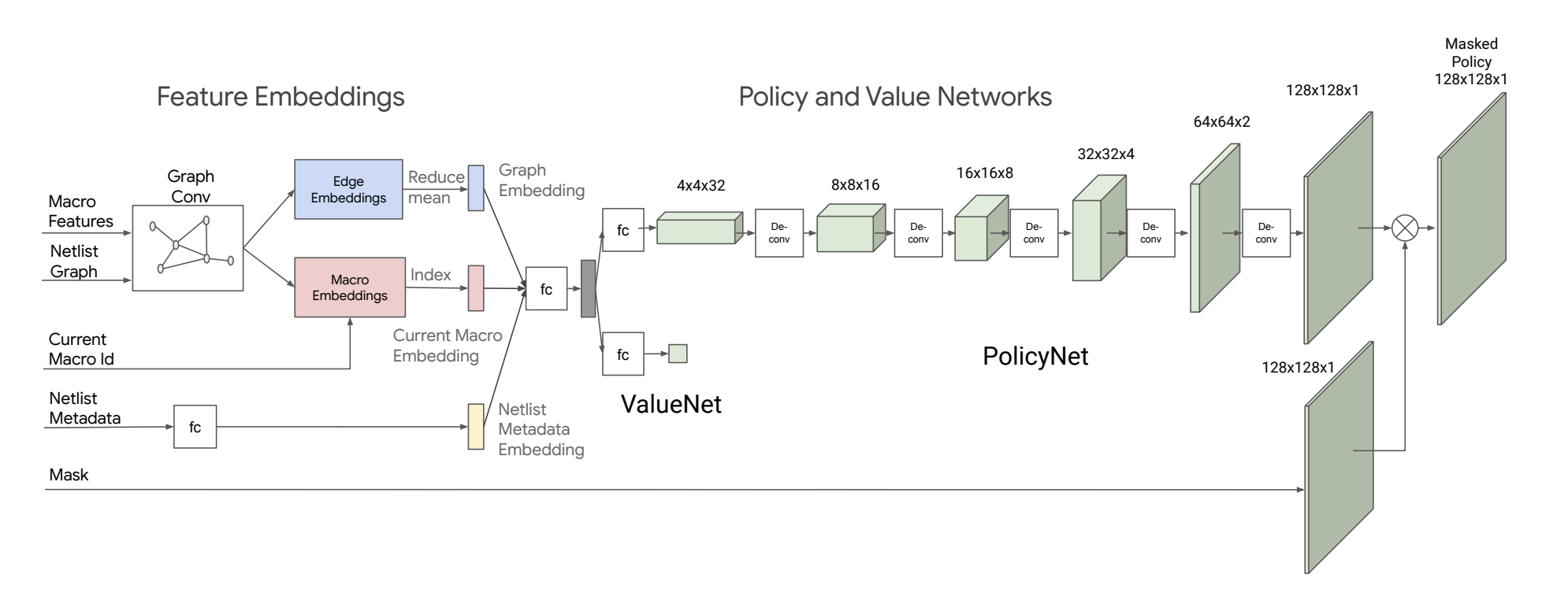
논문에서 제안하고 있는 모델[1]은 크게 (1) 환경으로부터 전달받은 Observation에서 중요한 정보들을 추출하여 State Representation으로 만드는 State Encoder와 (2) State Representation을 바탕으로 적절한 Action을 결정하는 Policy and Value Network 두 부분으로 나누어 볼 수 있습니다.

강화학습 모델이 현재 상태를 이해하려면 무엇이 필요할까

위의 그림에서 확인할 수 있듯이 에이전트는 매 Step마다 환경으로부터 다음 다섯가지 정보를 전달받아 이를 기준으로 최적의 Action을 선택하게 됩니다.

Macro Feature
Netlist Graph
Current Macro id
Netlist Metadata
Mask

각각에 대해 하나씩 살펴보면, Macro Feature는 배치 대상되는 Macro의 특성 정보들을 말합니다. 여기서의 특성 정보에는 Macro의 타입, 크기, 위치 정보등이 포함되어 있습니다. 두 번째 정보인 Netlist Graph는 소자들의 연결관계를 표현하는 Adjacency Matrix입니다. 세 번째 Current Macro id는 현재 배치하고자 하는 Macro가 무엇인지 알려주는 정보입니다. 네 번째 Netlist Metadata는 말 그대로 Netlist의 메타 정보들로서, Netlist를 구성하는 Macro의 개수, Wire의 개수, Standard Cell Cluster의 개수, 배치 Grid의 크기 등이 들어갑니다. 마지막으로 Mask는 배치가 가능한 영역을 알려주는 정보로, Action을 Masking 하여 배치 배치 불가능한 영역에 대해서는 배치가 이뤄지지 않도록 합니다.

Netlist가 Graph니 GNN을 쓰자

강화학습이 잘 이루어지기 위해서는 환경으로 부터 전달받은 정보들을 적절히 처리하여 적절한 State Representation으로 만들 수 있어야 하는데, 이를 위해서는 입력 데이터와 문제의 특성을 고려하여 이를 추출하는 모델을 구성해야 합니다. 위에서 언급한 Observation 중에서 Macro Feature와 Netlist Graph는 전형적인 Graph 구조입니다. Macro Feature가 Graph에서 각 Node의 특성들을 표현하는 정보라면, Netlist는 해당 Node들이 어떻게 연결되어 있는지 알려주는 Adjacency Matrix라고 할 수 있기 때문입니다.

이러한 점에서 Graph 데이터를 잘 다루는 모델을 사용할 필요가 있는데, Graph Neural Network로 분류되는 GCN(Graph Convolution Network)[7] 등이 Graph 데이터를 효율적으로 처리하는 대표적인 모델들이라고 할 수 있습니다. 그런데 문제가 있다면 Critical Path의 계산과 같이 반도체 설계에 있어 중요한 몇몇 특성들은 Node에 대한 정보 만으로는 알 수 없고 Edge에 대한 정보가 필요한데, 최근 제안되고 있는 많은 GNN의 방법들이 Node feature를 추출하는 구조로 되어 있다는 것입니다[10].

“We find that other graph network approachs are much more focused on the features of the nodes. Our problem is actually more about the function of the edges, something like about the critical path of the network. It is not really about the node features themself, so we took an edge based approach”(Lecture by Azalia Mirhoseini & Anna Goldie)

따라서 Chip Placement 논문에서는 Chip Placement 문제에 맞게 Node Feature와 더불어 Edge Feature도 함께 뽑아낼 수 있는 새로운 방법[10]을 제시하고 있습니다.

\[\eqalign{ &\text{While not converged do} \\ & \qquad \text{Update edge: } e_{ij} = fc_1 (\text{concat}[ fc_0(v_i) \vert fc_0(v_j) \vert w_{ij}^e ]) \\ & \qquad \text{Update node: } v_i = \text{mean}_{j \in N(v_i)}(e_{ij}) \\ &\text{end} }\]

위의 수식에서 \(v_i\)는 \(i\) 번째 Macro에 대한 Embedding을, \(e_{i,j}\)는 \(i\)와 \(j\) 번쩨 Macro를 잇는 Wire에 대한 Embedding을 의미합니다. 두 수식을 모든 Macro와 Wire에 대해 수렴할 때까지 반복적으로 적용하여 최종적인 Embedding으로 \(v\)와 \(e\)를 사용하게 됩니다. Node Embedding과 Edge Embedding을 함께 얻을 수 있다는 점이 위 구조의 주요 특징이라고 할 수 있습니다.

위 Model Architecture 이미지를 기준으로 보면 \(v\)가 붉은 색의 Macro Embedding이고, \(e\)가 푸른 색의 Edge Embeddings 입니다. Node Embedding에 대해서는 Indexing을 하고 있는데 각 Node의 특성을 가지고 있는 정보이므로 현재 배치할 Node의 정보만을 추출하는 것으로 이해할 수 있습니다. Edge Embedding에 대해서는 Reduce Mean을 하는데 이를 통해 전체 Graph의 특성을 담고 있는 Vector를 만들 수 있습니다.

“We can get a representation of the entire graph by just taking the mean of the all edge embeddings”(Lecture by Azalia Mirhoseini & Anna Goldie)

이와 관련하여 Google의 Chip Placement 논문 1 저자인 Azalia Mirhoseini와 Anna Goldie는 강연[10]에서 위와 같이 표현하고 있습니다.

모두 합쳐 State Representation을 만들자

에이전트가 Action을 선택하는 데에 사용하는 정보라고 할 수 있는 State Representation은 다음 세 가지 정보를 Concatnation하여 만들게 됩니다.

Graph Embedding
Current Macro Embedding
Netlist Metadata Embedding

Graph Embedding과 Current Macro Embedding은 앞서 확인한 GNN 구조의 두 출력 값 Macro Embedding과 Edge Embedding으로 구해집니다. 구체적으로는 Graph Embedding은 Edge Embedding을 Reduce Mean한 것이고, Current Macro Embedding은 Current Macro id를 Index로 Macro Embedding에서 뽑아낸 것입니다. 마지막으로 Netlist Metadata Embedding은 Fully Connected Network를 통해 구할 수 있습니다.

업데이트 알고리즘은 PPO

Policy의 역할은 현재 주어진 Macro를 Chip Canvas 상의 어떤 지점에 배치할 것인지 결정하는 것입니다. 이때 Grid 형태의 확률 함수를 효과적으로 표현하기 위해 Deconvolution Layer를 Policy Network에 사용한 것으로 보입니다.

Policy Network를 직접 업데이트해야 하기 때문에 Policy Gradient 계열의 업데이트 알고리즘을 사용해야 하는데, 상대적으로 적은 연산량과 높은 성능 그리고 분산 학습에 강점을 보이는 PPO 알고리즘[3]을 사용하고 있습니다[11].

State Representation을 더 잘 만드는 방법: Transfer Learning

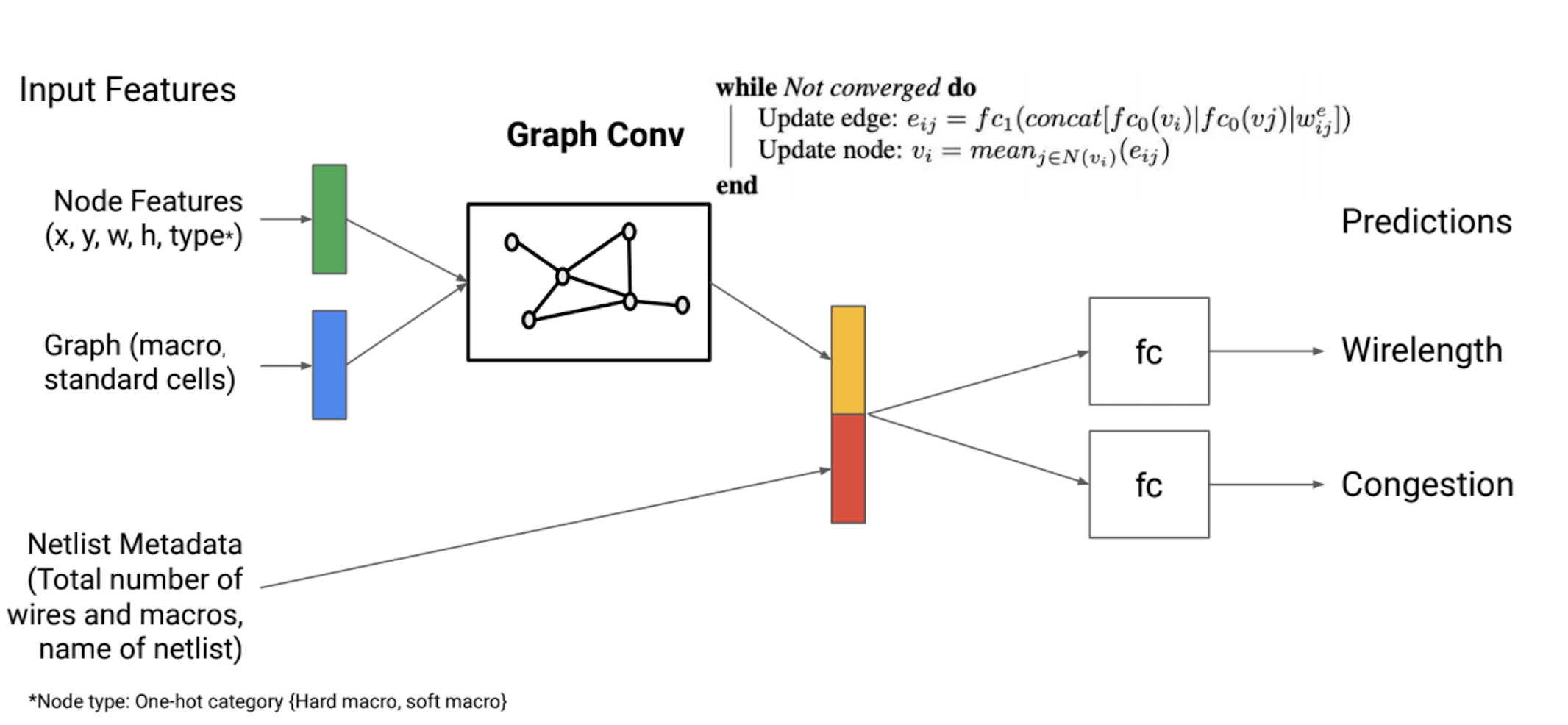
모델의 학습과 관련하여 한 가지 특이한 점이 있다면 모델의 앞단이라고 할 수 있는 State Encoder 부분을 Supervised Learning으로 미리 업데이트 한 후에 사용한다는 점입니다. 에이전트가 환경의 현재 상태를 이해하고, 그에 맞춰 최적의 Action을 선택하는 데에 State Representation을 이용한다는 점에서 이를 잘 표현하는 것이 중요합니다. 그런데 State Encoder 부분을 Policy와 함께 처음부터 업데이트하게 되면 초기 Observation에 대해서는 잘 대처할 수 있을지 모르나 학습 과정에서 Policy가 접하게 되는 새로운 Observation에 대해서는 적절하게 표현하지 못할 수도 있습니다.

이러한 문제를 보완하려면 State Encoder가 다양한 Observation을 사전에 경험하는 것이 좋습니다. Google의 Chip Placement 논문에서는 이러한 점에서 Transfer Learning을 제안하고 있으며, 다양한 배치 결과를 입력으로 하여 해당 배치의 Reward를 예측하도록 Pre-Training을 진행하게 됩니다. 구체적인 Pre-Training 도식은 Google의 Chip Placement 논문 1 저자인 Azalia Mirhoseini와 Anna Goldie의 강연 [10]에서 나온 위 이미지를 참고하시면 좋을 것 같습니다.

논문에서 제시하는 실험과 결론

논문에서는 제시하고 있는 방법론과 관련하여 다양한 실험을 진행하고 그 결과를 정리하고 있습니다. 다만 배치 대상이 Google TPU이고 수백 개의 Macro와 수백만 개의 Standard Cell로만 구성되어 있다고만 언급하고 있을 뿐 구체적인 사양은 보안 문제로 공개하지 않고 있습니다.

Transfer Learning이 정말 효과적일까?

첫 번째는 State Encoder를 위해 Pre-Training이 효과적인지 검증하는 실험입니다. 이를 위해 논문에서는 다음 네 가지 경우에 대한 실험 결과를 비교하고 있습니다.

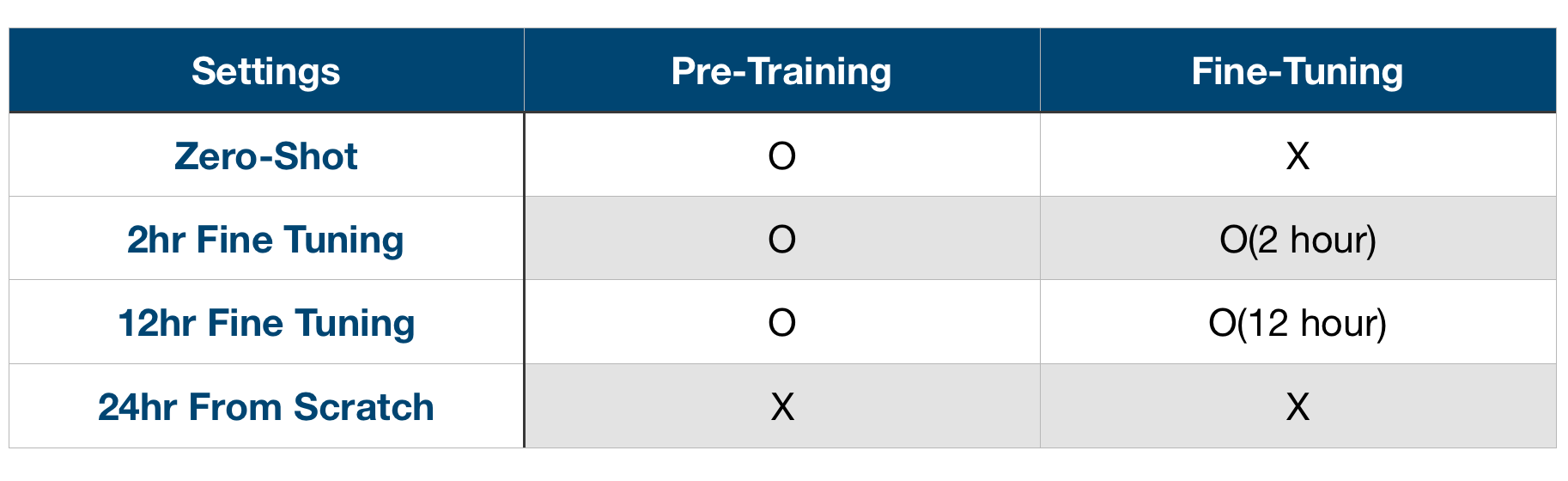
위의 네 가지 실험 조건은 Pre-Training과 Fine Tuning을 기준으로 하고 있습니다. 여기서 말하는 Pre-Training이란 구체적으로 미리 확보한 데이터를 사용하여 State Encoder가 Reward를 Regression 할 수 있도록 Supervised Learning을 수행하고, 이렇게 학습된 State Encoder를 Policy Network 앞단에 붙여 사용하는 것을 말합니다. 그리고 Fine Tuning이란 Pre-Training을 수행하여 일부 레이어가 학습된 상태로 전체 모델에 대한 업데이트를 시작할 때, 미리 학습된 레이어도 함께 업데이트하는 것을 의미합니다.

이에 대한 실험 결과는 다음과 같습니다. y축이 Placement Cost인 만큼 작으면 작을 수록 좋습니다.

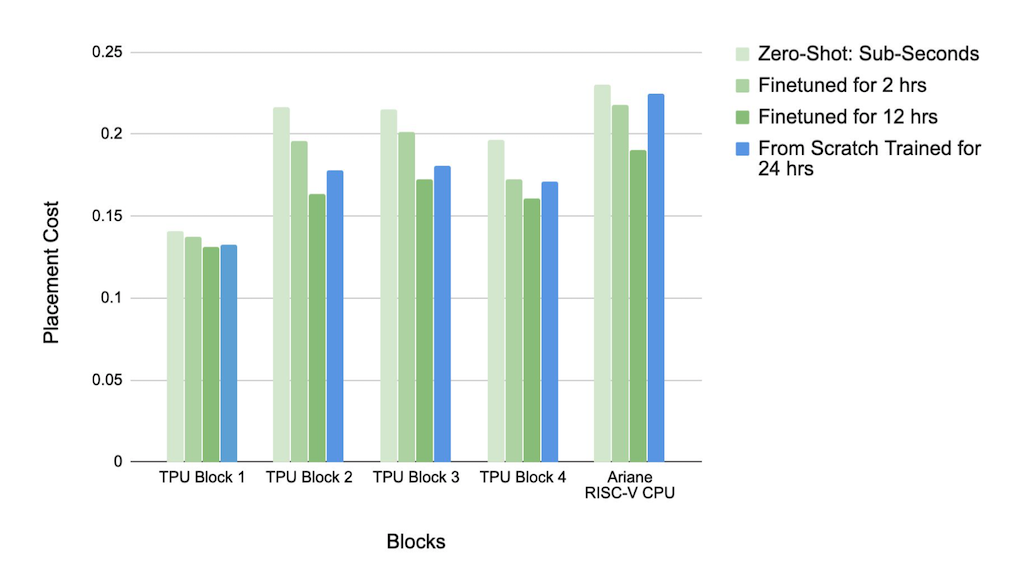
모든 Netlist에 대해 Pre-Training을 수행한 후 12시간 동안 Fine Tuning을 추가적으로 진행했을 때 가장 성능이 좋음을 알 수 있습니다.

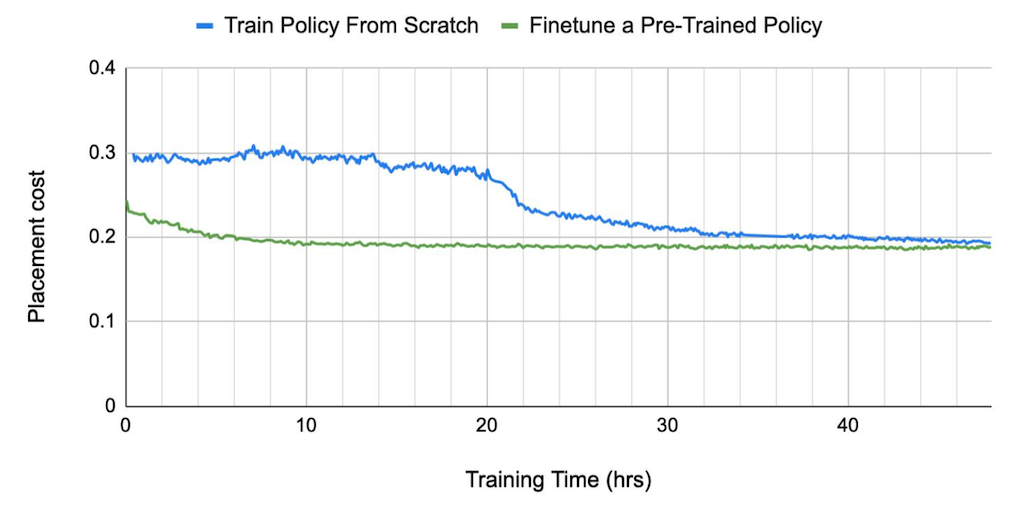
위의 그래프는 초록선으로 표현되는 Pre-Training 방법과 파란선의 From-Scrach 방법 간의 수렴 속도를 비교하고 있으며, 이를 통해 Pre-Training을 수행했을 때 수렴 속도가 월등히 빠르다는 것을 확인할 수 있습니다. 이러한 점에서 Pre-Training과 Fine Tuning을 통해 최대한 많은 종류의 배치 결과를 학습한 에이전트가 배치 성능이 가장 좋으며, 수렴 속도 또한 빠르다고 할 수 있습니다.

Transfer Learning에 사용하는 데이터는 다다익선

Pre-Training의 목표는 State Encoder가 다양한 Observation을 경험하여 적절한 State Representation을 만들 수 있도록 하는 것입니다. 따라서 다양한 상황이 담기도록 데이터셋을 구성하는 것이 중요합니다. 이와 관련하여 Google의 Chip Placement 논문에서는 Netlist(TPU Block)의 종류를 2개부터 20개까지 늘려가며 실험을 진행했고, 그 결과 Training Set의 크기가 작을수록 Policy Network가 빠르게 오버피팅 되는 문제가 발생함을 확인할 수 있었다고 합니다. 실험 결과는 아래와 같습니다.

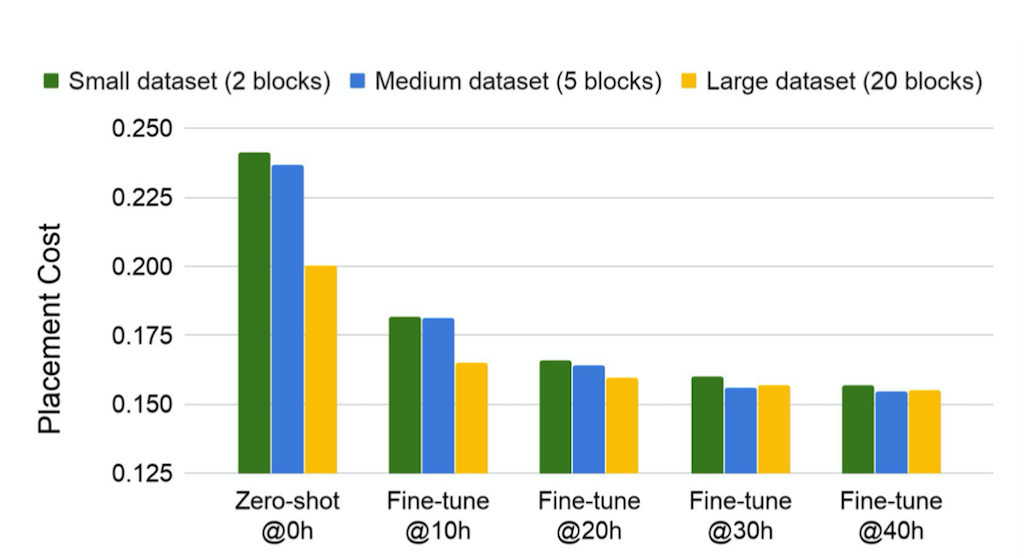
위의 도표를 되면 거의 모든 경우에서 Train Set의 크기가 클수록 성능이 좋아지는 경향을 보이며 특히 Fine Tuning을 적게 수행했을 때 그 차이가 더욱 도드라짐을 알 수 있습니다.

사람보다 더 낫다

마지막으로 SOTA로 알려져 있는 배치 알고리즘 RePlAce[6]와 전문가가 직접 수행하는 방법과 비교하는 실험을 진행하고 그 결과를 정리하고 있습니다. Ours로 표기된 것이 논문에서 제시하고 있는 방법을 사용한 것으로, 20개의 TPU Block을 대상으로 Pre-Training을 진행하고 5개의 Test TPU Block에 대해 Fine Tuning하여 얻은 수치라고 합니다. 그리고 Manual이 전문가 팀이 직접 EDA tool을 사용하여 반복적으로 개선하여 얻은 결과입니다.

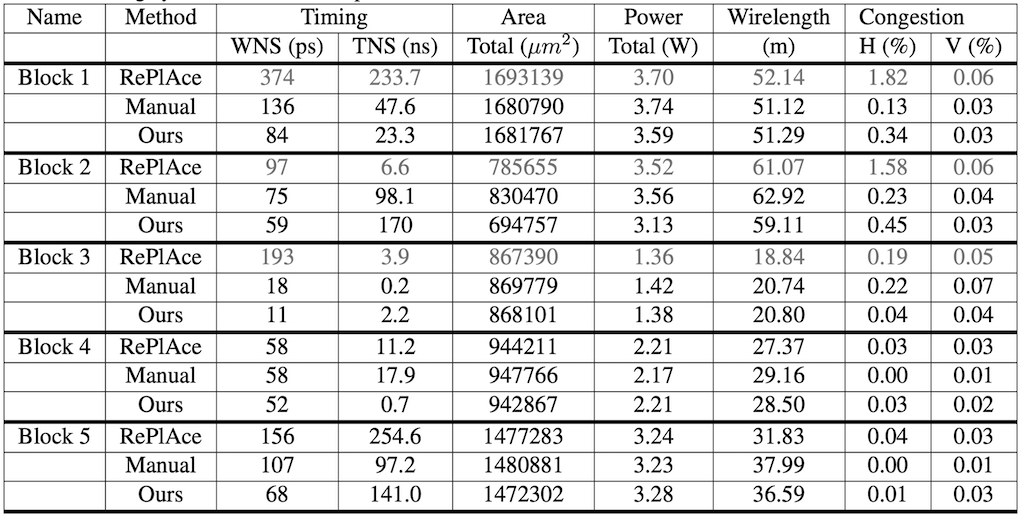
테이블2의 메트릭을 정확하게 이해하기 위해서는 각각이 무엇을 의미하는지 정확하게 알아야하는데, 여기서 표를 이해하는 데에는 WNS가 100ps 이상이거나 Horizontal/Vertical Congestion이 1%를 넘기면 사용할 수 없는 배치가 된다는 점만 알아두시면 될 것 같습니다. 이러한 기준에 따르면 Block 1,2,3에 대한 RePLAce의 배치 결과는 이를 초과하여 사용할 수 없기 때문에 논문의 저자들은 자신들이 제안하는 방법론이 가장 뛰어나다고 결론내립니다.

다만 학습 속도에 있어서는 RePlAce가 보다 나은 방법으로, 1시간에서 3.5시간 정도 걸리는 데에 비해 논문의 방법은 학습시간까지 모두 포함하여 3시간에서 6시간 정도 걸렸다고 합니다.

결론

Google의 Chip Placement 논문은 다음 네 가지 면에 있어서 큰 의미를 가지고 있습니다.

Chip Placement를 강화학습 문제로 정의한 점
주로 수작업으로 처리했던 Macro 배치 과정을 자동화했다는 점
전문가 및 기존 알고리즘과 비교해 볼 때 높은 성능을 보였다는 점
Transfer Learning 기법 등을 도입하여 학습 속도 및 성능을 끌어올린 점

특히 전문가가 수주에 걸쳐 완성한 배치 결과보다 논문을 통해 제안하고 있는 강화학습 기반 알고리즘이 6시간 만에 만들어낸 배치 결과가 더 좋았다는 점을 강조하며 마무리하고 있습니다.

MakinaRocks COP 팀에서는 Google의 Chip Placement 논문의 아이디어를 FPGA에 적용하는 프로젝트를 진행했습니다. 상용 EDA Tool과 비교하여 성능을 개선한 사례가 궁금하시다면 아래 링크에서 확인하실 수 있습니다.

Chip Placement on FPGA 프로젝트를 소개합니다! (written by 우경민)

Chip Placement with Deep Reinforcement Learning 연구의 뿌리라고도 할 수 있는 Neural Combinatorial Optimization with Reinforcement Learning에 대해서도 별도 포스팅으로 정리해봤습니다.