주문형 반도체 (ASIC) Floorplan 자동화 - Part II

Written by Wooshik Myung on 03 Dec 2021

프로젝트 소개

placement animation — FIGURE ABSTRACT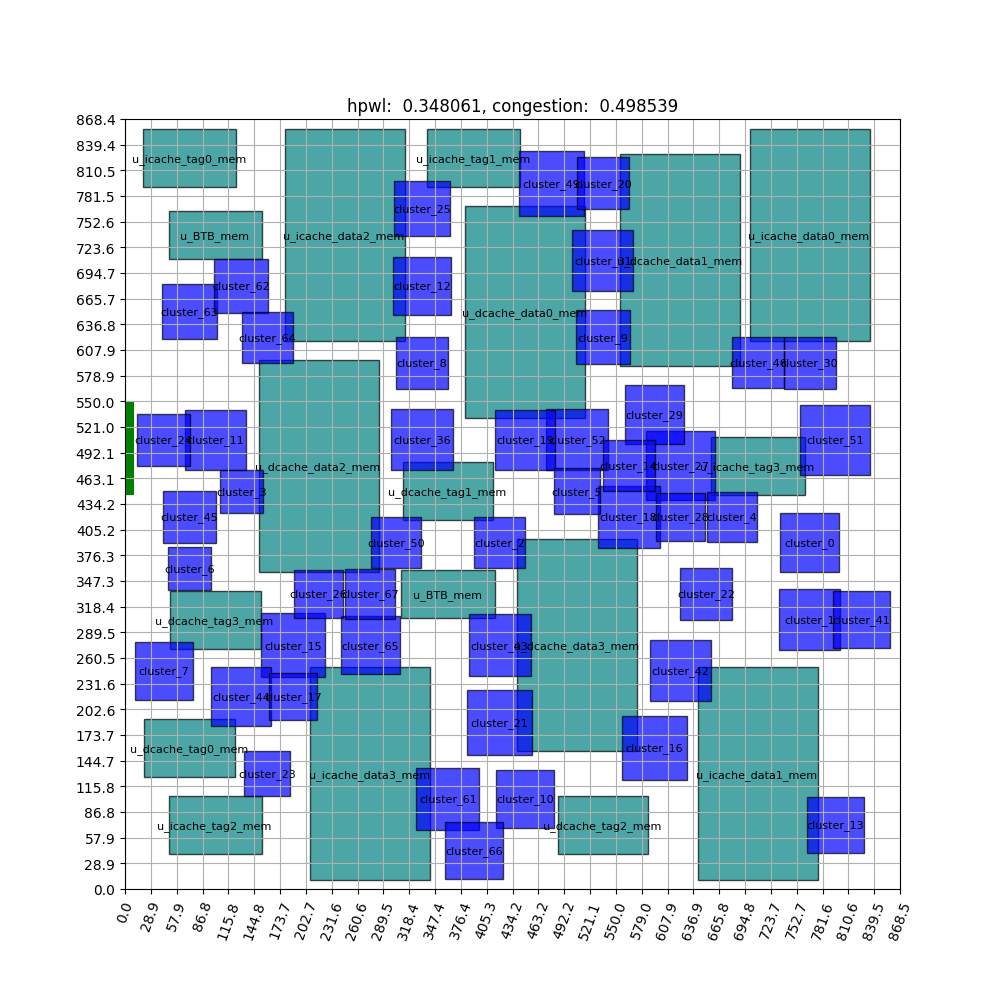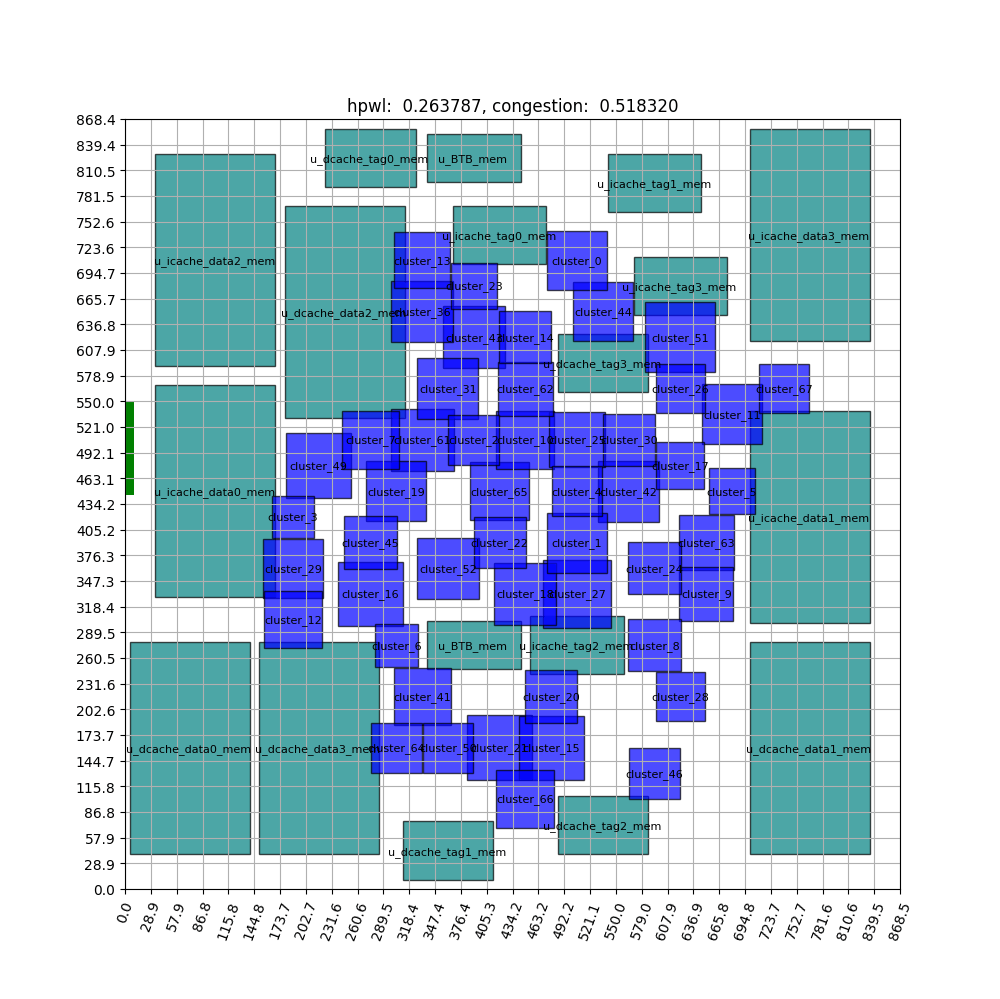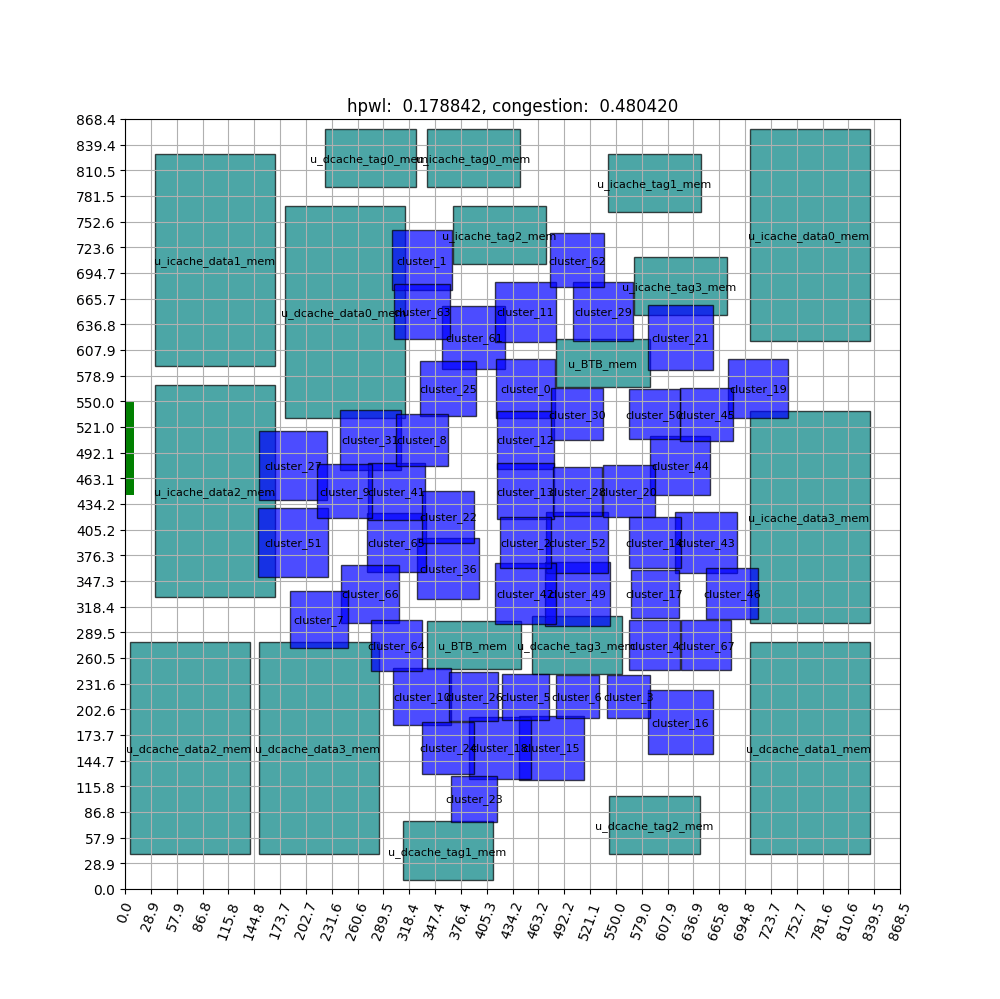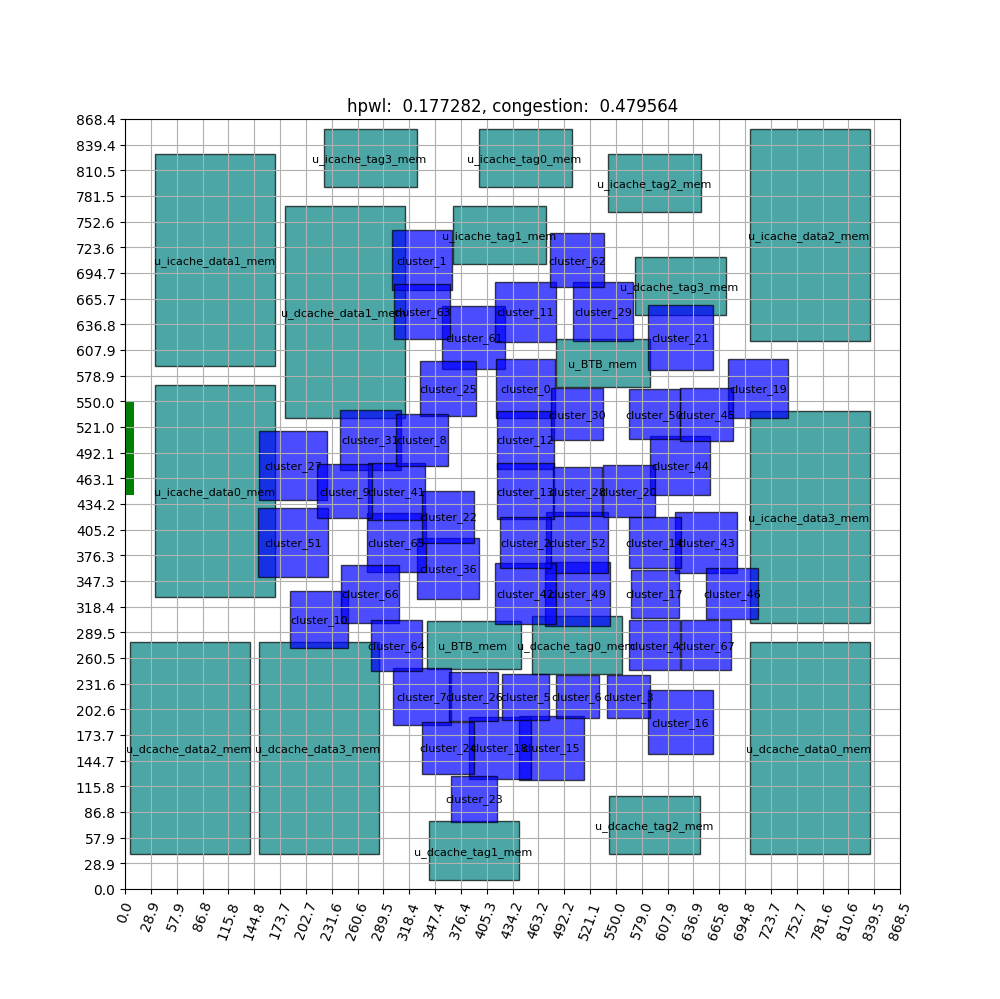
위 애니메이션은 약 1500 iterations 정도의 학습 과정을 보여주고 있습니다. 녹색의 큰 사각형은 Macro, 청색의 작은 사각형은 Standard Cell Cluster를 나타냅니다. 어느 정도 학습이 진행된 후, 사각형의 움직임이 눈에 띄게 줄어들며 안정된 모습을 보여줍니다. 에이전트는 Macro는 Chip Canvas 영역의 바깥쪽, Standard Cell Cluster는 안쪽에 위치시키도록 학습합니다. 위 실험을 하기까지의 과정에 대한 자세한 설명은 본 포스팅을 참고해주세요.

Introduction

본 프로젝트의 목적은 강화학습을 이용해 주문형 반도체 (Application-Specific Integrated Circuit, ASIC)의 제조 공정 중 하나인 Floorplan 단계에서의 배치 최적화 문제를 해결하는 것입니다. 주요 기술 내용은 지난 2020년 6월 구글에서 발표해 Nature 등재로 화제가 되었던 A graph placement methodology for fast chip design[1][2] 논문에 기초를 두고 있습니다. Floorplan은 트랜지스터가 아닌 블록 단위의 배치를 하는 과정이며, 수십~수백만 개 단위의 트랜지스터와의 연결성을 고려하며 블록들을 배치해야 하기 때문에 시간이 많이 소요되는 작업 중 하나입니다. 본 포스팅을 통해 약 5개월간 경험한 Floorplan 문제의 이해부터 솔루션 구현까지의 과정을 공유드리려고 합니다.

먼저 본문에서 자주 언급하는 주요 용어들과 뜻입니다.

Macro: Floorplan 과정에서 배치되는 소자의 종류 중 하나, 메모리 구성 요소로 Standard Cell 대비 훨씬 큰 크기를 가지고 있음
Standard Cell: NAND, NOR, XOR과 같은 논리 게이트, 크기가 매우 작으며 수십~수백만 개 단위의 소자가 사용됨
Net: Macro와 Standard Cell들의 연결 관계를 정의하는 Wire
Netlist: Net들의 집합체

Is this a Real Problem?

Floorplan 과정은 일반적으로 사람의 손에 의해 수행됩니다. Chip Canvas라는 2차원의 연속 공간에서 복잡한 연결 관계를 고려하며 수백 개에 달하는 Macro들을 배치하는 작업은 큰 탐색공간(Search Space)으로 인해 높은 복잡도를 가지고 있는 문제입니다. 또한, 직접 Macro를 배치한 후 그 뒤의 설계과정을 전용 Electronic Design Automation(EDA) Tool을 통해 수행하고 나서야 배치에 대한 평가를 할 수 있습니다. 만약 평가 결과가 좋지 않다면, Macro를 배치하는 작업부터 다시 수행해야 하므로 기술자의 숙련도에 따라서 필요한 시간이 크게 달라지곤 합니다. 또한 숙련된 기술자라도 며칠에서 몇 주의 시간을 소요하기도 합니다. 현업에서 종사하시는 전문가분들과의 협업을 통해 알게 된 Floorplan의 주요 문제점은 아래와 같이 정리할 수 있습니다.

Macro의 배치를 수작업으로 진행 후, EDA Tool을 이용해 결과를 확인하는 작업을 여러 번 반복해야 하는 만큼 시간이 오래 걸림
사람의 경험이 매우 중요하기 때문에, 숙련도에 따라 품질과 요구되는 시간의 편차가 큼

이 포스팅에서는 문제정의와 해결 방법 관련된 기술적인 내용을 중점적으로 설명합니다. (연구 배경 및 의의에 대한 더욱 자세한 설명은 ASIC-Chip-Placement 1부을 참고해주세요.)

How to solve?

기존의 배치 최적화 문제*에 적용되는 많은 Classic한 방법들(Simulated Annealing[3], Genetic Algorithm[4]…)은 좋은 성능을 보여주지만, 새로운 문제를 만나면 같은 도메인이라도 초기 상태부터 다시 최적화를 진행해야 한다는 단점이 있습니다. 한번 학습된 모델이 다르게 정의된 문제에서 별다른 추가 학습 없이 어느 수준 이상의 해답을 찾는 것을 일반화(Generalize)라고 합니다. 많은 연구[8][9]에서 인공 신경망을 적용한 강화학습은 강력한 Generalize 수준을 보여주고 있습니다. 강화학습의 이러한 강점을 이용한다면 여러 구조와 크기의 Netlist에 대해서 추가적인 학습 없이 또는 최소한의 학습 시간만을 가지고 좋은 배치를 찾을 수 있습니다. (예: 소자 5개, 10개로 구성된 Netlist 들의 배치를 학습하여 20개 규모의 Netlist에 대해서도 일정 수준 이상으로 배치) 저희는 이점에 주목하여 강화학습을 주요 알고리즘으로써 사용했습니다. 본 포스팅에는 최종 목표(Gneneralization)에 도달하기에 앞서, 강화학습을 사용한 단일 Netlist의 Floorplan 학습 과정을 소개합니다.

* 배치 최적화 문제: 대상의 물리적인 위치를 통해 목표함수를 최적화하는 문제

강화학습이란?

강화학습은 에이전트(Agent)가 환경(Environment)과 상호작용에서의 시행착오(Trial and Error)를 통해 더 높은 보상(Reward)을 얻을 수 있는 행동(Action)들을 학습하는 알고리즘입니다. 환경은 에이전트의 행동마다 다음 상태(State)와 보상을 반환하며, 에이전트는 전달받은 상태를 고려해 다시 행동을 결정하게 됩니다. 강화학습은 Markov Decision Process[5] (MDP)에 기반해, 차례로 어떤 의사결정(Decision Process)을 해야 하는 문제들에 많이 적용됩니다.

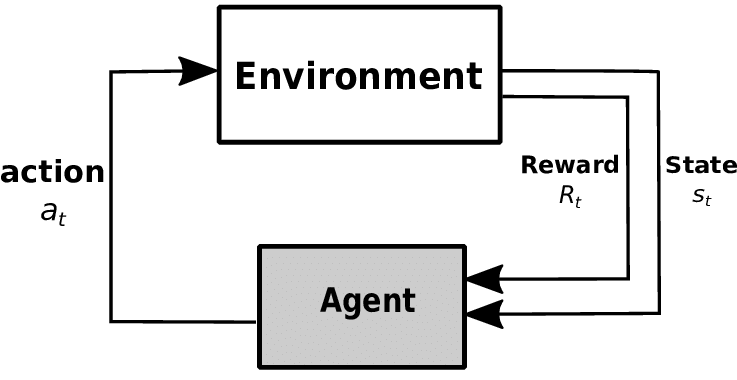
markov decision process — [그림 ] - Markov Decision Process

결국 에이전트는 학습하는 과정 중에 Sampling 되는 모든 에피소드(Episode)*에 대한 보상의 기댓값을 최대화하기 위한 행동들을 학습합니다. 당연하게도, 강화학습은 그 구성 요소들(에이전트, 상태, 행동, 보상)의 정의방법에 따라 다른 학습양상을 보여줍니다. 아래에서는 저희가 환경과 에이전트를 어떻게 정의했는지 설명하겠습니다.

* 에피소드: 에이전트가 일련의 행동들을 수행하고 보상들을 얻는 (상태, 행동, 보상)의 Sequence, 에피소드가 종료되면 환경은 초기상태로 리셋된다.

Technical Overview

먼저 환경과 모델이 어떻게 동작하는지 전체적인 흐름을 설명하고 이후 강화학습의 각 요소에 대해서 구체적으로 정의하겠습니다.

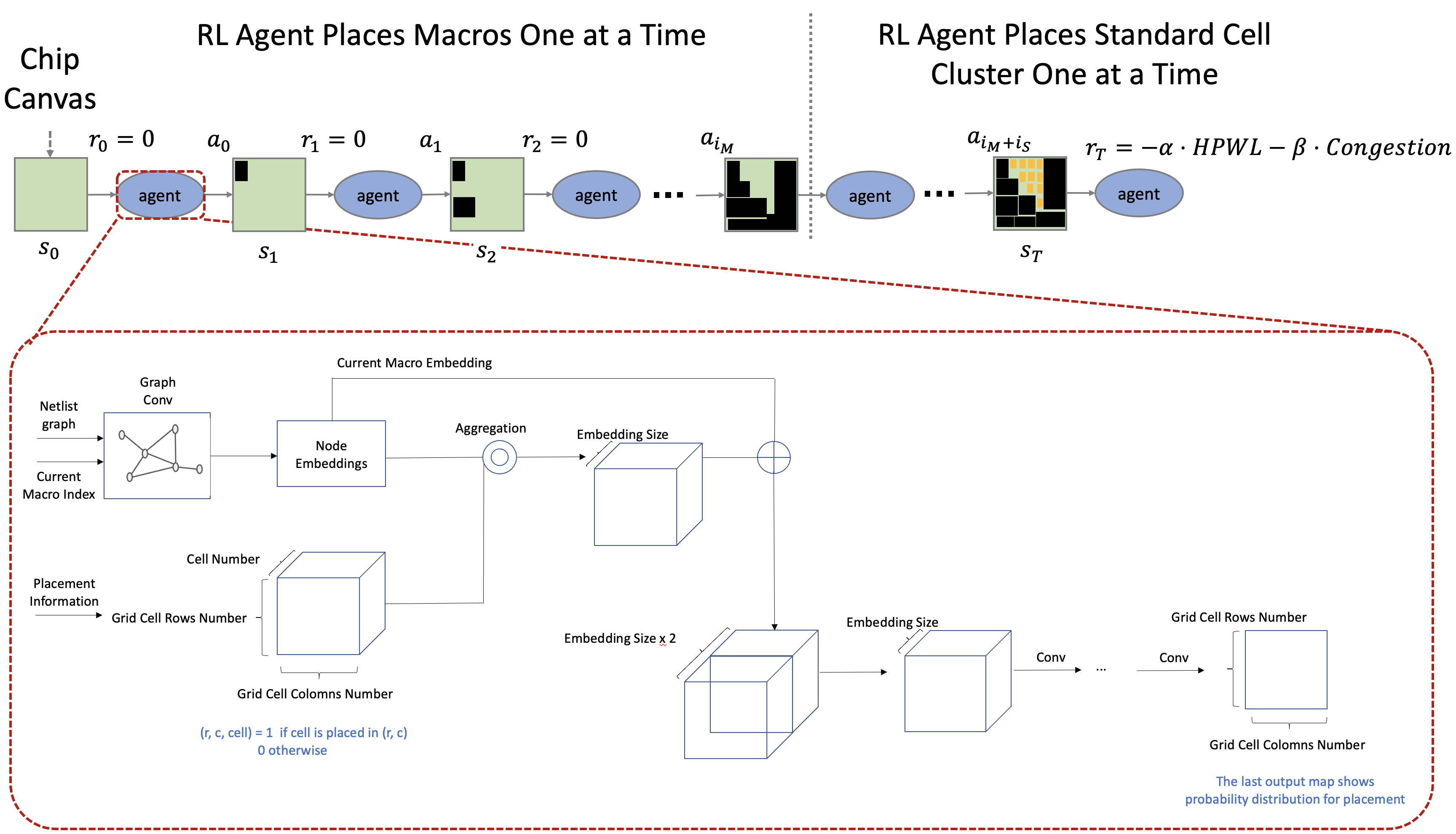
환경 정의

에이전트는 환경의 주요 구성요소인 상태, 행동, 보상을 통해 환경과 상호작용하며 학습합니다. 그러므로 에이전트를 효과적으로 학습시키기 위해서는 각 요소를 적절히 정의해야 합니다. 배치 최적화에서 환경의 각 요소는 아래와 같은 역할을 수행해야 합니다.

상태: 행동을 결정하기 위한 판단에 필요한 정보를 담고 있어야 함
행동: 더 좋은 Chip Design을 얻을 수 있게 하는 행동의 집합
보상: Chip Design의 품질

저희가 설계한 환경은 아래와 같은 순서로 진행됩니다.

빈 Chip Canvas인 초기 상태에서 시작하여 행동 한 번에 소자 한 개를 배치
마지막 배치 외의 모든 배치에 대해 0의 보상을 반환
1~2번 반복 후, 모든 소자들의 배치가 완료되면 보상을 계산
1~3번 반복하며 학습 진행

상태, 행동, 보상 정의을 정의하기에 앞서 모델 설계를 먼저 알아보도록 하겠습니다.

모델 설계

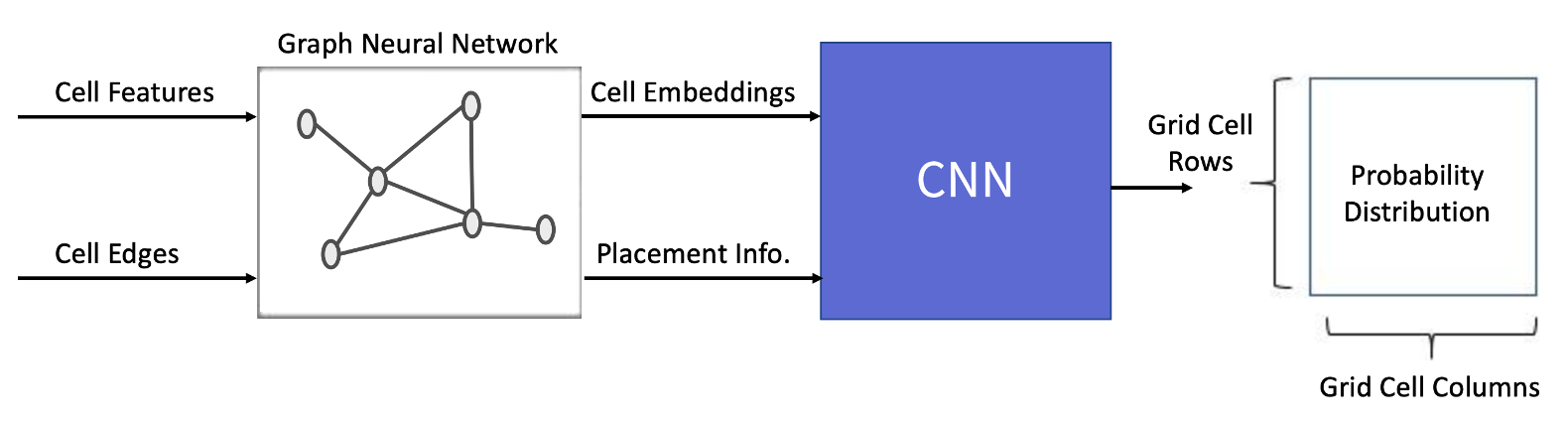
뉴럴넷 모델은 환경으로부터 전달받은 상태의 정보들을 인식해 행동을 결정할 확률분포를 계산하는 역할을 수행합니다. 이 프로젝트의 경우, 소자의 물리적 특성과 연결정보를 바탕으로 이미 배치된 소자들에 대한 정보와 앞으로 배치할 소자들에 대한 정보를 알아야 합니다. 이를 구현하기 위해, Graph Neural Network(GNN)과 Convolutional Neural Network(CNN)으로 이루어진 모델을 설계했습니다. 각각의 목적은 아래와 같습니다.

GNN: Graph 형태의 Netlist의 정보를 효과적으로 Embedding하기 위해 선택했습니다
CNN: 배치가 완료된 소자들의 지역적인 정보를 효과적으로 학습할 수 있는 CNN 구조를 선택했습니다

모델의 각 구조에 대한 자세한 설명은 Model Description 장에서 드리도록 하겠습니다.

강화학습 환경 정의하기

State Representation

상태는 현재 환경이 어떤 상태에 있는지에 대한 정보를 담고 있습니다. 상태는 에이전트가 좋은 행동을 결정하기 위해 도움이 되는 정보들을 전달해야 합니다. 칩 설계의 전문가분들이 소자들의 연결 관계와 물리적 특성을 고려해 배치하는 것에 착안하여 에이전트가 다음 행동을 결정하기 위해 필요한 정보를 아래와 같이 정의했습니다.

소자들 간의 연결 관계
각 소자의 물리적 정보 (width, height, is_macro, n_pins … etc.)
이번에 배치할 소자의 정보
지금까지의 배치 정보

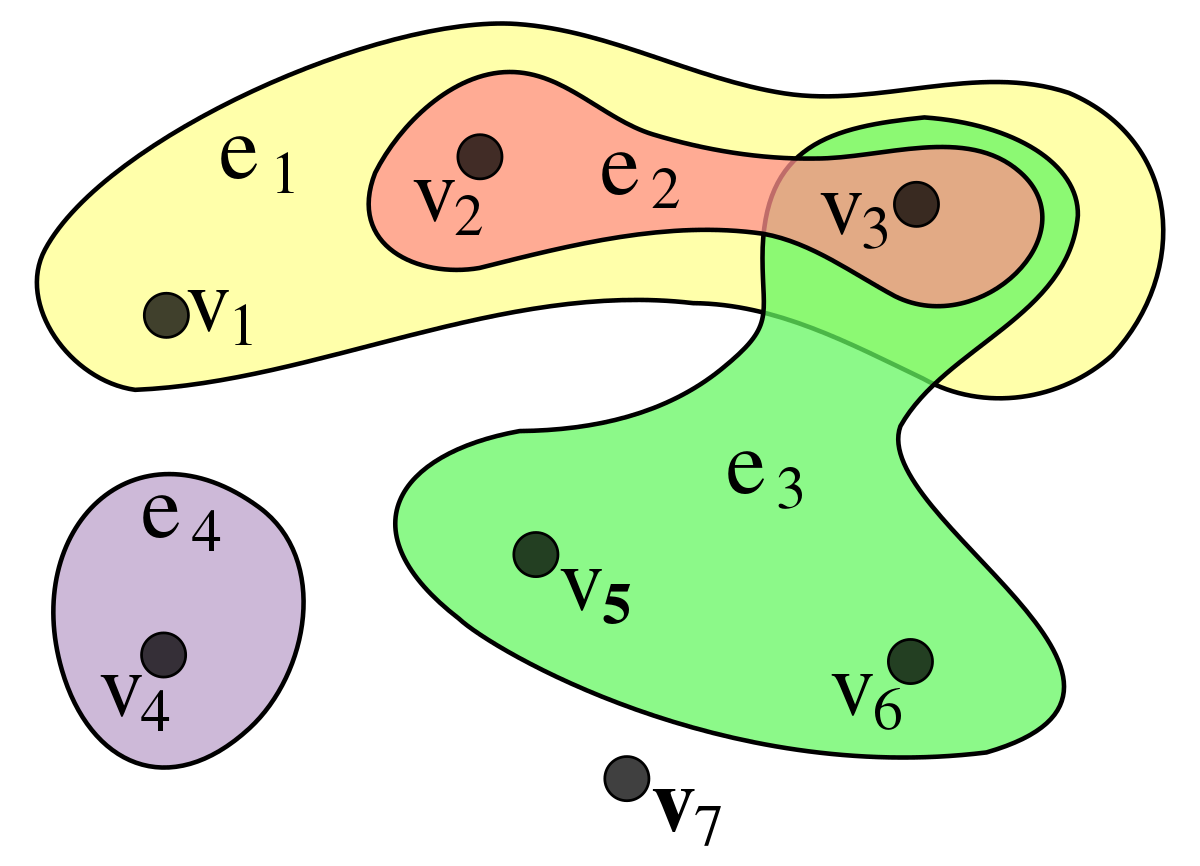
각 소자들 간의 연결 관계가 아래와 같은 Hypergraph*의 형태를 띠고 있는 만큼, 소자들의 물리적 특성들을 Node Features로 정의할 수 있습니다.

* Hypergraph: 한 Edge에 둘 이상의 Vertex가 연결되어 있는 그래프 구조

수백개 단위의 Macro를 배치하는 것에 비해, 수십~수백만 개 단위의 Standard Cell들을 배치하는 일은 굉장히 높은 복잡도를 가지고 있습니다. Standard Cell을 배치하는 과정을 간소화 하기 위해 소자들을 Clustering 합니다. Clustering을 진행하면 배치하려는 대상의 개수가 줄어들어 문제 복잡도가 감소합니다. 저희는 Hypergraph를 graph로 변환할 때 발생하는 정보손실을 최소화하기 위해 Hypergraph Clustering Algorithm인 hMETIS[6] 알고리즘을 사용했습니다. 추후 배치 과정에서 한 Cluster에 속해있는 소자들을 묶어 하나의 독자적인 소자로 취급합니다.

Action Representation

행동은 에이전트가 상태의 정보들(소자들의 물리적 특성, 현재 배치상태 등)을 이용해 현재 배치할 소자를 어느 위치에 둘 것인지 결정짓는 역할을 합니다. 에이전트가 얻는 보상을 최대화하기 위해서는 충분한 탐험(Exploration)이 필요합니다. 탐험을 효율적으로 하기 위해서는 적절한 크기의 탐색공간을 정의해야 합니다. 저희는 이러한 점들을 고려해 연속공간의 Chip Canvas를 2차원 Grid의 이산 공간으로 정의했습니다. 에이전트가 Neural Network로부터 얻어진 확률분포에서 특정 Grid Cell*을 선택하면 배치될 소자의 중앙이 해당 Grid Cell의 중앙에 위치하도록 구현했습니다.

* Grid Cell: 2차원 Grid에서 한 칸에 해당하는 단위

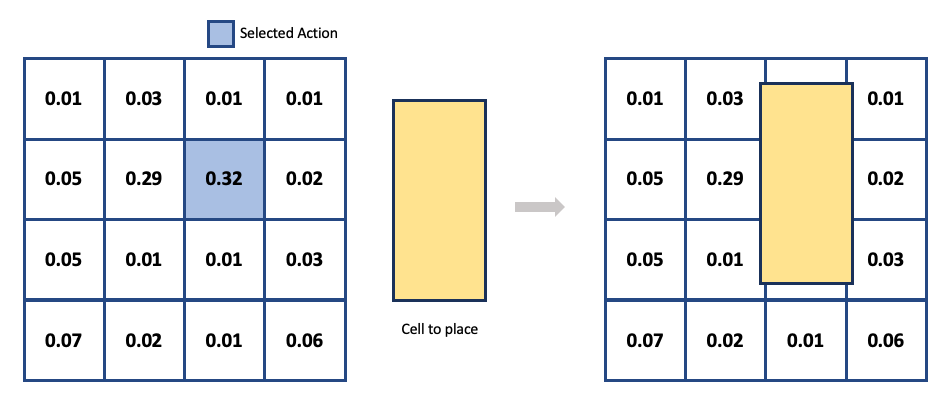
Canvas를 Grid로 정의하면 탐색공간을 줄이면서 배치 결과를 평가하기 위한 Approximated Metric을 단순하게 정의할 수 있다는 장점이 있습니다. Grid로 정의할 때 고려되어야 할 아래 issue들을 어떻게 해결했는지는 APPENDIX를 참고해주세요.

A.1. Grid Cell Size Decision
A.2. Invalid Action Masking

Reward Representation

보상은 에이전트에게 수행한 행동이 얼마나 유익한지를 알려주는 중요한 요소입니다. 일반적으로 ASIC의 Floorplan 결과는 ICC2와 같은 전용 EDA Tool을 사용하여 측정됩니다. Floorplan 이후의 배치 결과를 평가하기 위해 EDA Tool에서 수행하는 추가 설계과정은 보통 수 시간이 소요됩니다. 강화학습은 다량의 샘플을 통해 학습하는 방법이기 때문에 계산 속도를 고려했을 때 Tool의 결과를 직접적으로 보상으로써 정의하기에는 다소 무리가 있습니다. 그렇기 때문에 동일 시간 내에 더 많은 Sample을 확보하기 위하여 빠른 시간 내에 배치결과의 품질을 근사하는 함수를 설계해야 합니다.

배치결과의 품질을 적절히 근사하려면 먼저 좋은 배치가 무엇인지를 알아야 합니다. 산업에서는 일반적으로 PPA (Performance, Power, Area)라는 기준들을 사용합니다. 각 항목에 대응되는 효과는 아래와 같습니다.

Performance - 높은 클럭 주파수(Hz)
Power - 적은 전력 소모
Area - 작은 Chip Canvas

에이전트의 보상함수로 근사함수를 사용하기 위해서는 위의 3가지 사항이 모두 고려되어야 합니다. 언뜻보면 소자들을 가깝게 배치하면 데이터를 전달하는 Path의 길이가 짧아지면서 더 높은 Power, Performance와 더 낮은 Area를 얻을 수 있으리라 생각할 수 있습니다. 하지만, 소자들을 배치할 Chip Canvas에는 Routing Resources라는 것이 존재합니다. 이 말인즉슨, 소자끼리 Data를 주고받을 Routing Path가 필요한데 이를 지원하는 Routing Resources가 한정적이라는 것입니다. 그래서 소자들을 무작정 가깝게 배치해 단위 구역에 제공되는 Routing Resources보다 많은 Routing Path가 생기면 아래 그림처럼 다른 쪽으로 우회해서 신호를 전달해야 합니다.

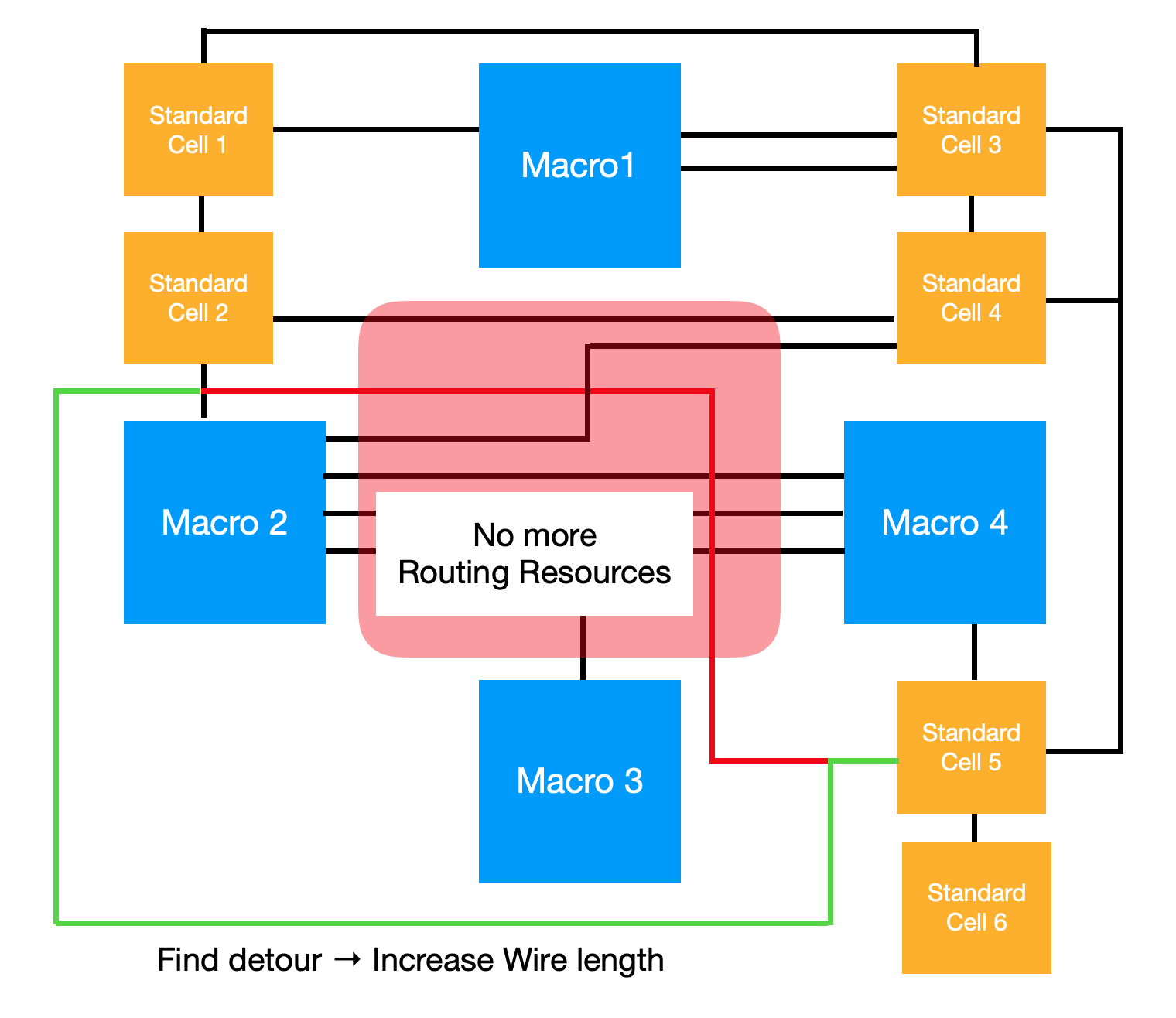
위의 그림에서 Macro 2와 Standard Cell 5의 가장 짧은 Routing Path가 적색 선입니다. 하지만 적색 영역에 너무 많은 Routing Path가 집중되어 있어 실제 신호 전달 시에는 녹색 선으로 우회해서 신호가 전달됩니다. 이러한 예시를 통해 우리의 목표를 아래와 같이 정의할 수 있습니다.

'소자들의 거리(Wire Length)는 최대한 가깝게 하되, 한곳에 너무 많은 Routing path(Congestion)들이 몰리지 않게 !'

위의 목표를 생각해 봤을 때, 배치 최적화 문제는 소자들의 위치는 최대한 가까워야 하지만, 또 너무 근접하면 안 되는, Multi-objective Optimization Problem 입니다. 이를 달성하기 위해 설계한 보상함수는 아래와 같습니다.

\[R_{p,g}=-\alpha \cdot WireLength(p,g) - \beta \cdot Congestion(p,g) \qquad \text{S.t. } \text{density*}(p,g) \leq \text{max}_\text{density}\]

* Density: 단위면적에 배치되는 소자들의 밀도

Wire Length는 소자들을 가깝게 배치해주기 위한 역할, Congestion은 Routing Path들이 한곳에 너무 집중되지 않게 하기 위한 역할을 합니다. 아래 내용에서 각 항목이 어떻게 계산되고 적용되는지 설명합니다.

Wire Length

계산복잡도를 줄이기 위해 Wire Length를 근사한 Half-Perimeter Wire Length(HPWL)를 사용합니다. 모든 Net에 대하여, 각 Net에 속해있는 소자들에 대해 경계 상자를 그린 후, 그 둘레의 절반을 Wire Length로 근사하는 것입니다. HPWL은 가장 일반적으로 사용되는 Wire Length 추정 모델입니다. 계산이 매우 간단하고 소자의 Pin 수가 2 또는 3인 Net에 대해서 직교 Steiner Tree*를 사용해 얻어진 길이와 정확히 일치한다는 장점이 있습니다. 수식으로 표현하면 아래와 같습니다.

* 직교 Steiner Tree: Edge끼리 직각을 이루는 Steiner Tree, 소자들의 Wire Length를 추정할 때 가장 많이 쓰이는 방법 중 하나.

\[\begin{aligned} HPWL(i) = (\max_{b\in i}\{x_b\} - \min_{b\in i}\{x_b\} + 1) \\ + (\max_{b\in i}\{y_b\} - \min_{b\in i}\{y_b\} + 1) \end{aligned}\]

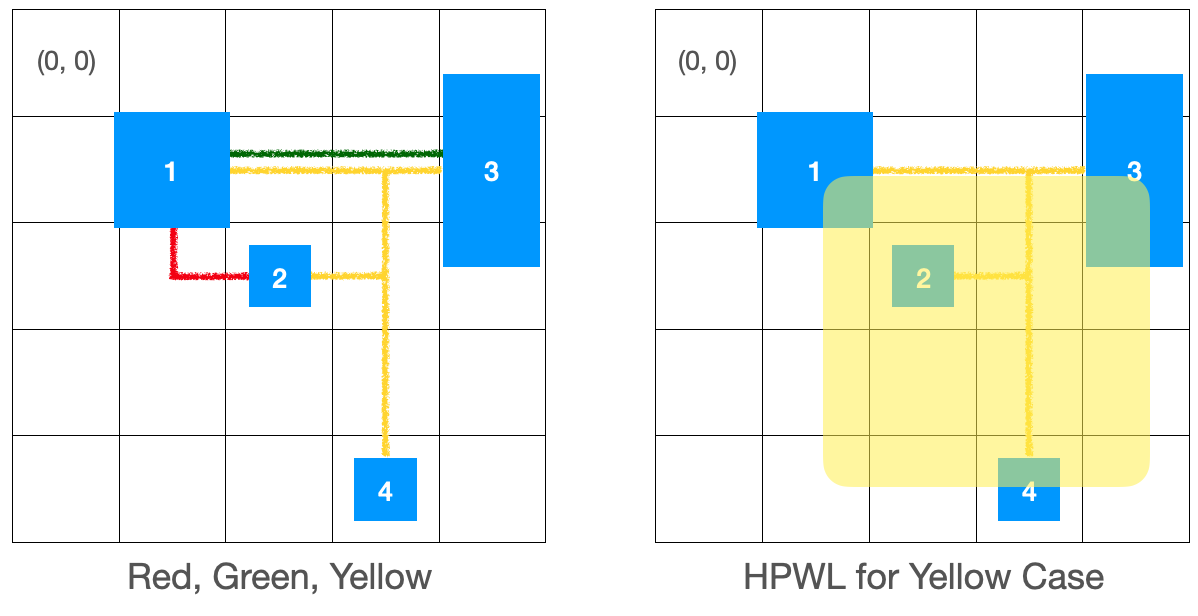
왼쪽의 그림에서 Routing Path의 색깔이 각기 다른 Wire를 나타낸다고 했을 때, HPWL은 아래와 같이 계산됩니다.

\[HPWL(Red)=(2 - 1 + 1) + (2 - 1 + 1) = 4 \\ HPWL(Green)=(4 - 1 + 1) + (1 - 1 + 1) = 5 \\ HPWL(Yellow)=(3 - 1 + 1) + (4 - 1 + 1) = 7\]

이렇게 전체 Wire Length의 근사치는 4 + 5 + 7 = 16이 됩니다. 이러한 계산방식으로 Net들의 Wire Length를 구합니다.

Example Code

def calculate_hpwl(net: Net) -> float:
  """Calculate HPWL given Net."""
  min_row, min_col, max_row, max_col = get_boundary_coordinate_of_net(net)
  hpwl = (max_row - min_row + 1.0) + (max_col - min_col + 1.0)
  return hpwl

Congestion

Congestion은 Routing Path들이 특정 지역에만 모이지 않게 하기 위해 적용됩니다. 전용 Tool을 이용해야만 정확한 측정이 가능한 지표로써, 저희가 환경 설계 과정에서 굉장히 많이 고민했던 부분이기도 합니다. Congestion은 특정 구역에서 제공되는 Routing Resources (supply)와 해당 위치에 놓인 Net의 Routing Path (demand)로 정의됩니다[7]. Horizontal과 Vertical의 Routing Resources는 독립적으로 고려됩니다.

[그림 ] - Congestion 정의[7]

Supply는 저희가 갖고 있는 데이터로는 측정할 수 없습니다. 따라서 Supply는 모두 일정하다고 가정하였습니다. 이러한 가정하에서 Congestion은 Demand에 의해 결정됩니다. 이러한 점을 고려해, 저희는 아래와 같이 계산한 Demand의 추정치를 Congestion 값으로 사용합니다.

congestion calculation flow — [그림 ] - Congestion 계산 과정

Example Code

def accumulate_local_congestion(
  global_congestion_map: np.ndarry,
  net: Net
) -> None:
  """Accumulate local congestions into the global congestion map."""
  # get edges through MST or Steiner Tree
  edges = get_edges(net)

  for edge in edges:
    # Calculate all path number to source / target for all grid cells.
    paths = get_paths(two_pnt_net)
    # Calculate partial congestion map horizontally and vertically
    congestion_maps = get_congestion_map(paths)
  global_congestion_map += congestion_maps

보상 함수 설계 시 고려되어야 할 Issue들은 아래 APPENDIX에 정리했습니다.

B.1. Normalization & Reward Coefficient
B.2. Invalid Episode Handling
B.3. Convolution Filter

Model Description

모델은 환경으로부터 전달받은 상태정보들을 활용해 행동을 결정하기 위한 확률분포를 계산합니다. State Representation에서 설명해 드린 것처럼 좋은 행동을 얻기 위해서 Netlist의 연결 구조와 현재 배치 상태 등을 인식해야 합니다. 이를 위해, GNN과 CNN으로 이루어진 2-Stage의 모델을 설계했습니다. GNN은 Netlist 정보를 Embedding 하고, CNN은 앞서 Embedding 된 정보와 현재 배치 상태에 대한 정보를 활용해 행동에 대한 확률분포를 계산합니다. 대부분의 GNN 모델들은 Ordinary Graph*를 Input Data로써 정의합니다. 그러므로, 범용적으로 쓰이는 GNN 모델들을 사용하기 위해 Hypergraph 형태의 Netlist를 Ordinary Graph로 바꿔주는 전처리를 진행합니다. 아래에서는 전처리 과정을 포함해 2-Stage 모델에 대해 설명합니다.

* Ordinary Graph: Edge하나에 Vertex 두 개가 연결되어있는 일반적인 형태의 그래프.

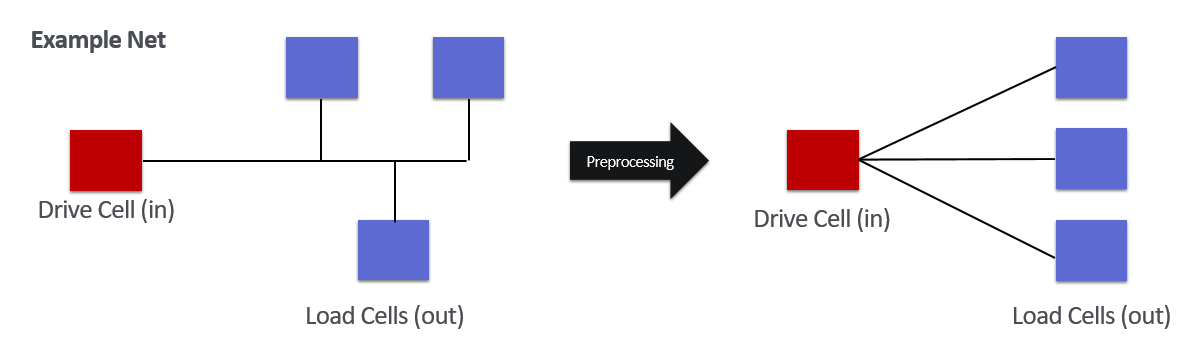
Hypergraph to Ordinary Graph

Ordinary Graph를 이용하는 범용적인 GNN 모델들을 보다 손쉽게 사용해보고 비교하기 위해 Hypergraph 형태의 Net을 Ordinary Graph의 형태로 바꿔줍니다. 이 과정에서 자연스레 연결 정보의 손실이 발생합니다. 손실되는 정보의 양을 최대한 줄이기 위해, 먼저 Net으로 연결된 Cell들의 특성을 알아야합니다. Hypergraph구조의 Net은 한개의 Drive Cell과 다수개의 Load Cell로 이루어져 있습니다. Drive Cell은 데이터를 받아서 Load Cell들에게 전달해주는 역할을 합니다. 이러한 특성을 고려하여, Hypergraph 형태의 Net을 Load Cell들이 Drive Cell에 각각 연결되어 있는 Ordinary Graph의 형태로 바꿔주는 전처리를 진행합니다.

Graph Features Embedding

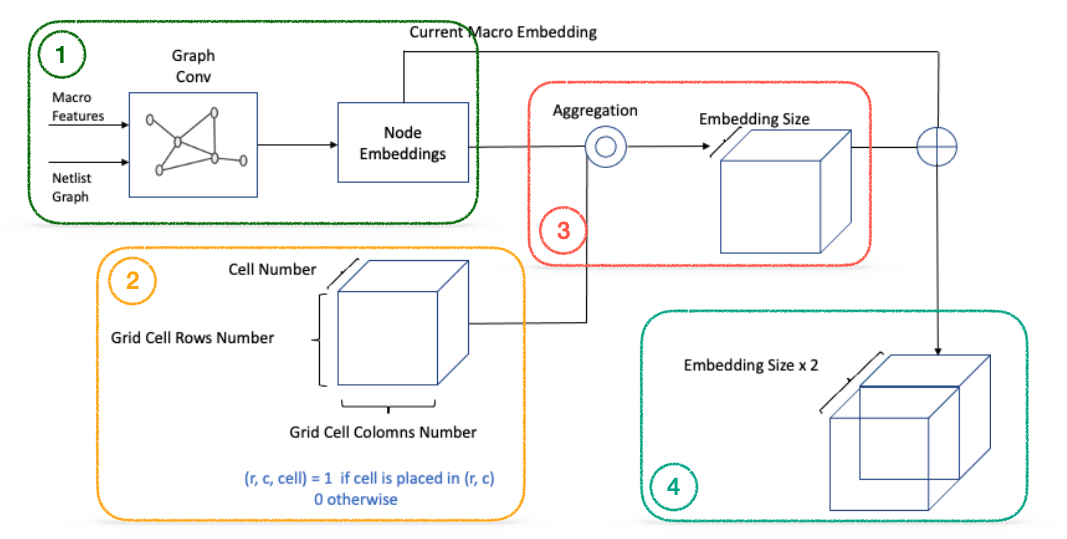
Graph Embedding — [그림 ] - Graph Feature Embedding

GNN은 그래프 형태로 표현된 Netlist 정보를 Embedding 해주기 위해 사용했습니다. Graph Feature embedding은 아래의 세부 단계를 거치며 수행됩니다.

Macro Features와 Netlist Graph를 GNN에 입력하여 Node Embedding을 추출
Placement Map에 각 소자들의 배치 현황을 표시 (각 row, col에 배치된 cell index의 값을 1로 설정, otherwise 0)
Placement Map의 정보를 바탕으로 Node Embedding을 Aggregation
3의 결과물의 채널에 배치할 Macro Embedding을 브로드캐스팅하여 Concatenation

즉, 각 Grid Cell에는 배치된 소자들의 Aggregated Embedding(현재 배치상태 + Netlist 연결정보)과 새로 배치할 Macro Embedding(현재 배치할 소자 정보)이 포함됩니다. 3차원의 Embedding 정보를 사용하면 CNN을 활용해 위치에 따른 지역 정보를 효과적으로 인식할 수 있다는 장점이 있고 이는 결국 적절한 배치영역을 찾을 수 있도록 정보를 제공합니다.

Action Decision

Graph Feature Embedding 된 정보를 하나의 이미지로써 인식해 다음 소자가 배치될 확률분포를 계산합니다. 마지막 Layer의 계산 결과에 Invalid Action Masking*이 적용되며, 해당 값들을 이용해 소자의 위치를 결정합니다. 이 과정은 아래 그림처럼 표현됩니다.

* Invalid Action Masking: 소자들이 놓인 상태에 따라 배치 가능한 위치를 결정해주는 작업. (APPENDIX A.2 참고).

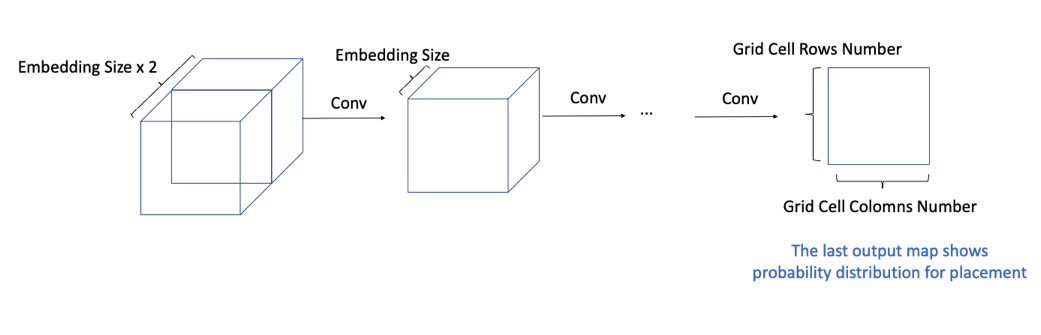
policy network — [그림 ] - Action Decision

Graph Feature Embedding을 CNN에 입력하여 점진적으로 채널을 1까지 줄입니다. Input Channel이 점진적으로 줄어드는 과정에서 Receptive Field는 커지므로, 모델의 깊이나 필터의 크기를 조절해 Chip Canvas의 전 영역을 모두 볼 수 있습니다. 마지막 Layer의 출력은 현재 소자를 배치할 위치에 대한 확률분포를 나타냅니다. 에이전트는 해당 확률분포에 따라 행동을 결정합니다.

Experiment Setup & Details

Dataset

강화학습의 효용성을 검증하기 위해 아래 Netlist를 사용했습니다. 상세 스펙은 아래와 같습니다(그림의 배치는 ICC2의 Macro Auto Placement 결과).

해당 Netlist는 18개의 Macro와 약 12만 개의 Standard Cell로 구성되어 있습니다. Standard Cell들을 50개의 Cluster로 압축한 후, 아래 기술된 실험을 진행했습니다. Graph Feature Embedding을 위해 Graph Convolutional Network(GCN) 모델을 사용했습니다.

Evaluations

실험의 복잡도를 줄일 수 있는 두가지 휴리스틱(Heuristic)을 적용할 수 있습니다.

Single Cluster

강화학습의 주요 목적은 Netlist의 복잡한 연결 관계를 고려하여 최적의 Macro 배치를 찾는 것입니다. Standard Cell에 대한 의존성을 줄이고 대략적인 Standard Cell의 위치에 대한 예측을 휴리스틱으로써 사용합니다. 모든 Standard Cell들을 하나의 Cluster로 묶어 배치를 수행하기 때문에 Episode 당 Step 수가 줄어들고 Macro와의 연결 관계가 단순해지므로 학습의 난이도가 감소합니다.

Bounding Box

일반적으로 Standard Cell끼리는 높은 연결 밀도를 가지고 있습니다. 실제 칩 배치 전문가들이 배치한 결과들을 살펴보면 대부분의 소자 배치 문제에서 Macro는 Chip Canvas의 바깥쪽 영역에, Standard Cell은 중앙 쪽에 위치합니다. 이러한 방식에 착안하여, Macro와 Standard Cell에 대해 개별적인 배치영역을 사용합니다. 학습초기에 Bounding Box를 설정하면 해당 영역에 Macro를 배치하지 않음으로써 탐색공간을 줄여 학습을 쉽게 만드는 효과를 얻을 수 있습니다.

Scenarios

학습 복잡도를 점차 늘려가며 강화학습의 효용성을 확인해보기 위해, 아래와 같은 시나리오로 실험을 설계했습니다.

Bouding Box + Single Cluster
Bouding Box
Vanilla RL w/o Heuristics

처음은 두가지 휴리스틱을 모두 적용 후, 하나씩 제거해 마지막은 별도의 휴리스틱 없이 강화학습만을 이용해 새로운 배치를 찾습니다.

Scenario1: Bounding Box + Single Cluster

첫번째로 진행한 실험은 시나리오들 중 가장 저복잡도로 볼 수 있는 Single Cluster와 Bounding Box를 취하는 것입니다.

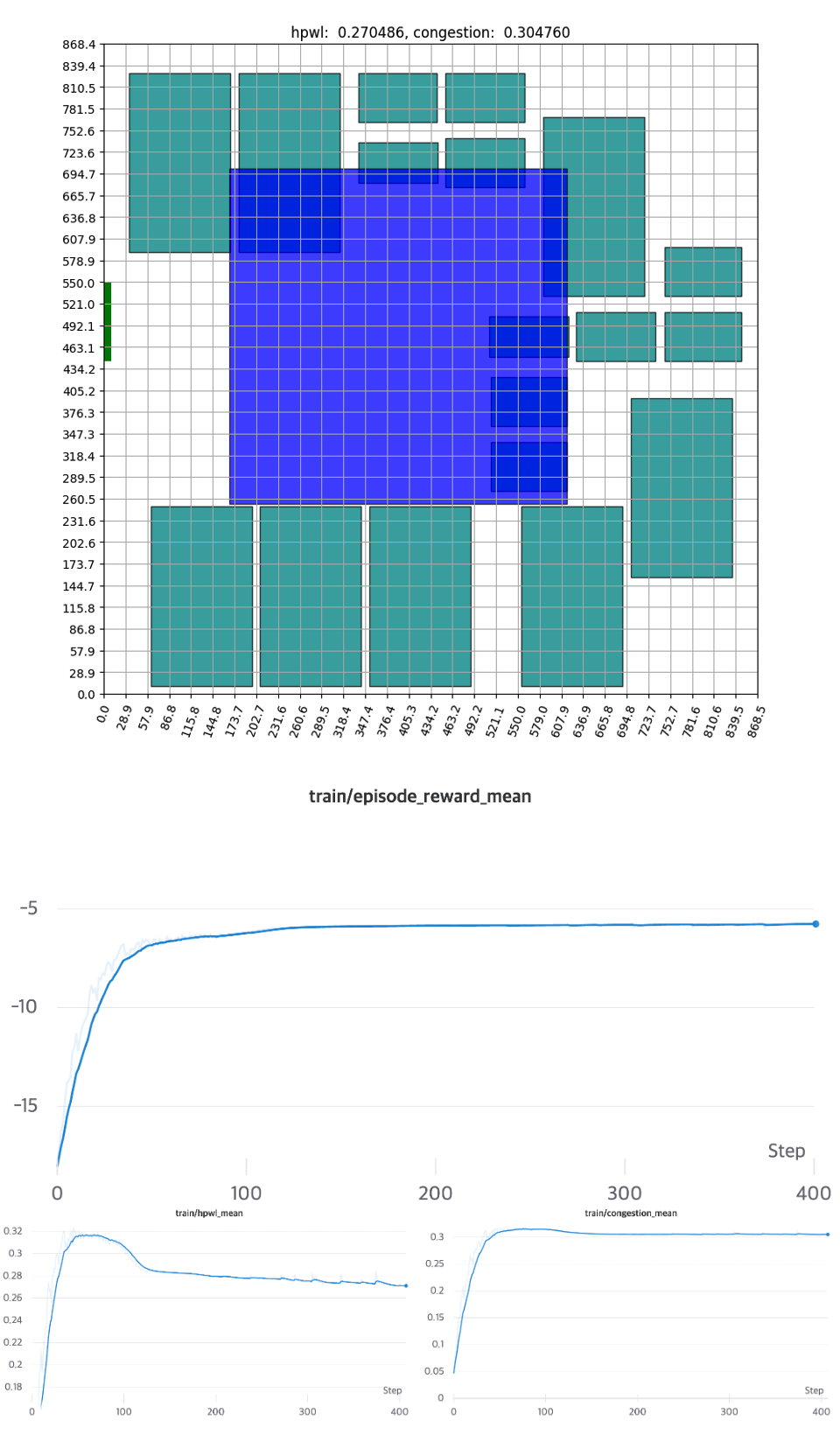
placment and training curve — [그림 ] - Single Cluster와 Bounding Box를 적용한 배치결과와 학습 곡선

Macro의 영역이 변두리에 할당된 만큼, 초기에 배치를 아예 찾지 못하는 확률(Invalid Episode*)이 증가합니다 그러면서 자연스레 초기의 HPWL, Congestion의 평균값은 매우 낮은 값으로 계산됩니다. 학습을 진행하면서, 점차 안정된 배치를 찾기 시작하고 약 150 Epochs 정도를 소모하며 수렴하는 모습을 보여줍니다. 해당 실험은 최소한의 복잡도에서 강화학습의 에이전트가 충분히 잘 작동하는 것을 알 수 있습니다.

* Invalid Episode: 모든 소자들이 배치되기 전에 배치 가능영역이 모두 사라지는 경우, HPWL과 Congestion은 0으로 계산되며, 보상은 $-\alpha-\beta$으로 주어진다. (APPENDIX B.2. 참고)

Scenario2: Bounding Box

두 번째로 진행한 실험은 첫 번째 시나리오에서 Cluster의 개수를 늘려 더 높은 복잡도에서 학습했습니다. Bounding Box만을 적용해 Macro와 Cluster의 위치변화에 보상이 더 예민하게 주어지도록 했습니다. 훈련 결과는 아래와 같습니다.

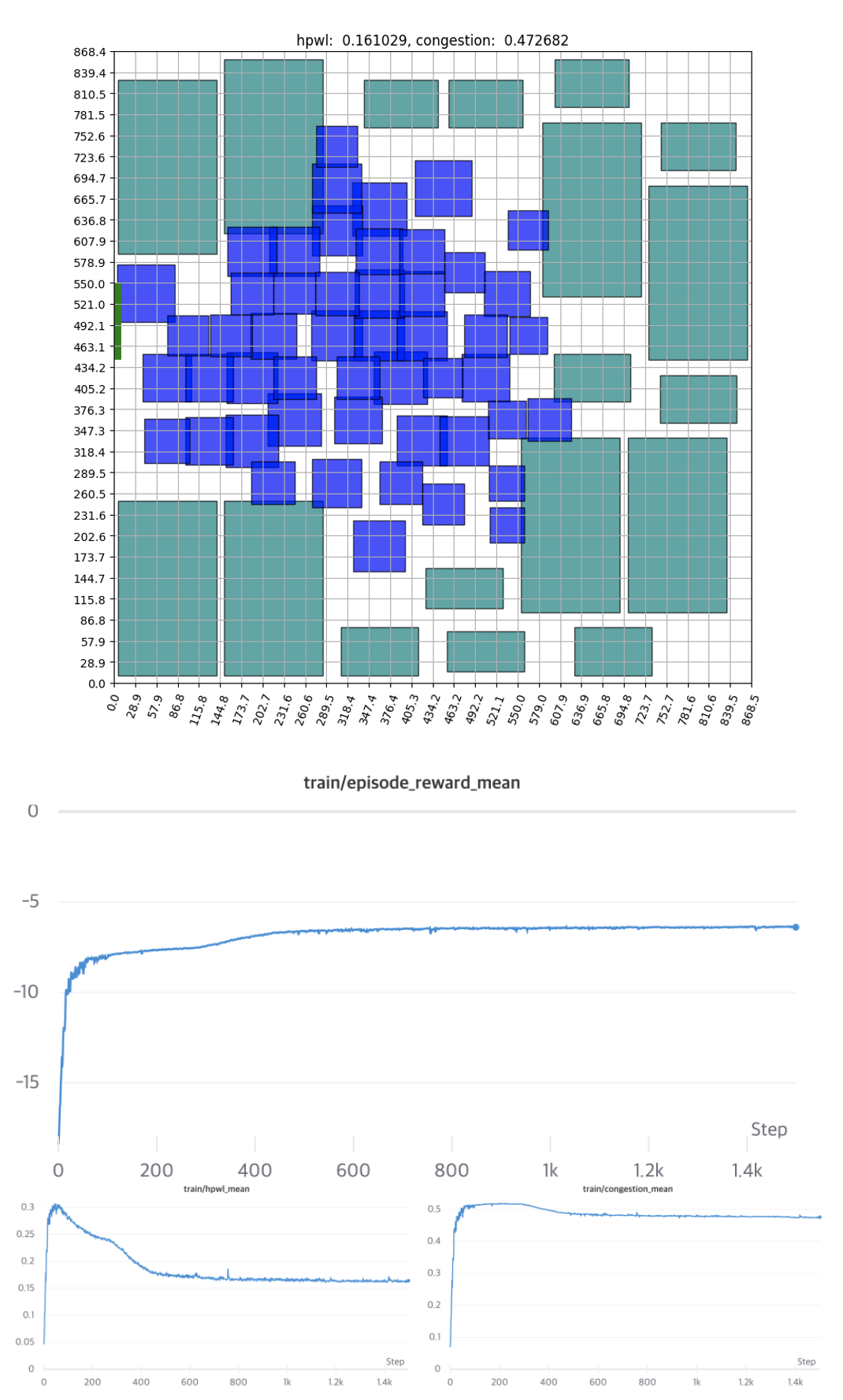
이번 시나리오 역시, Bounding Box의 영향으로 인해 초기에는 Invalid Episode가 많이 발생합니다. 하지만 이 역시 금방 해결되고 약 500 Epochs에서 수렴하는 것을 알 수 있습니다.

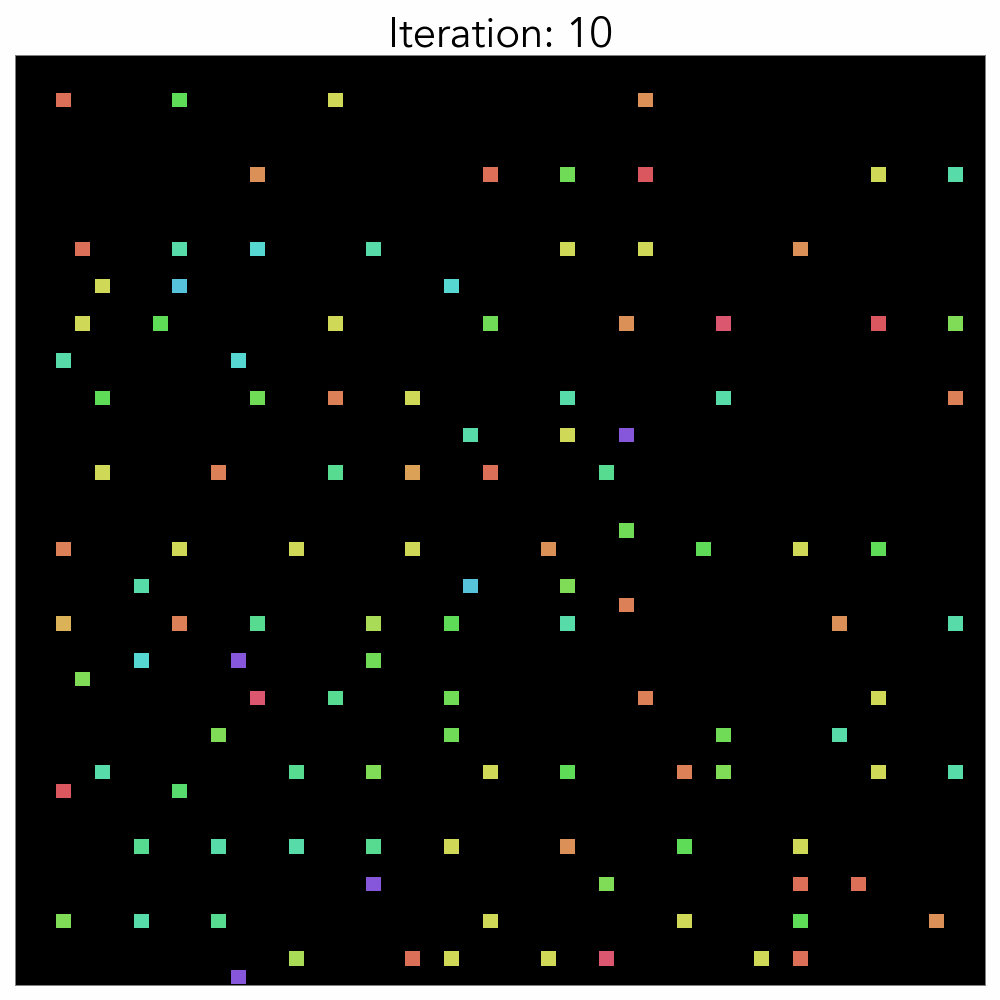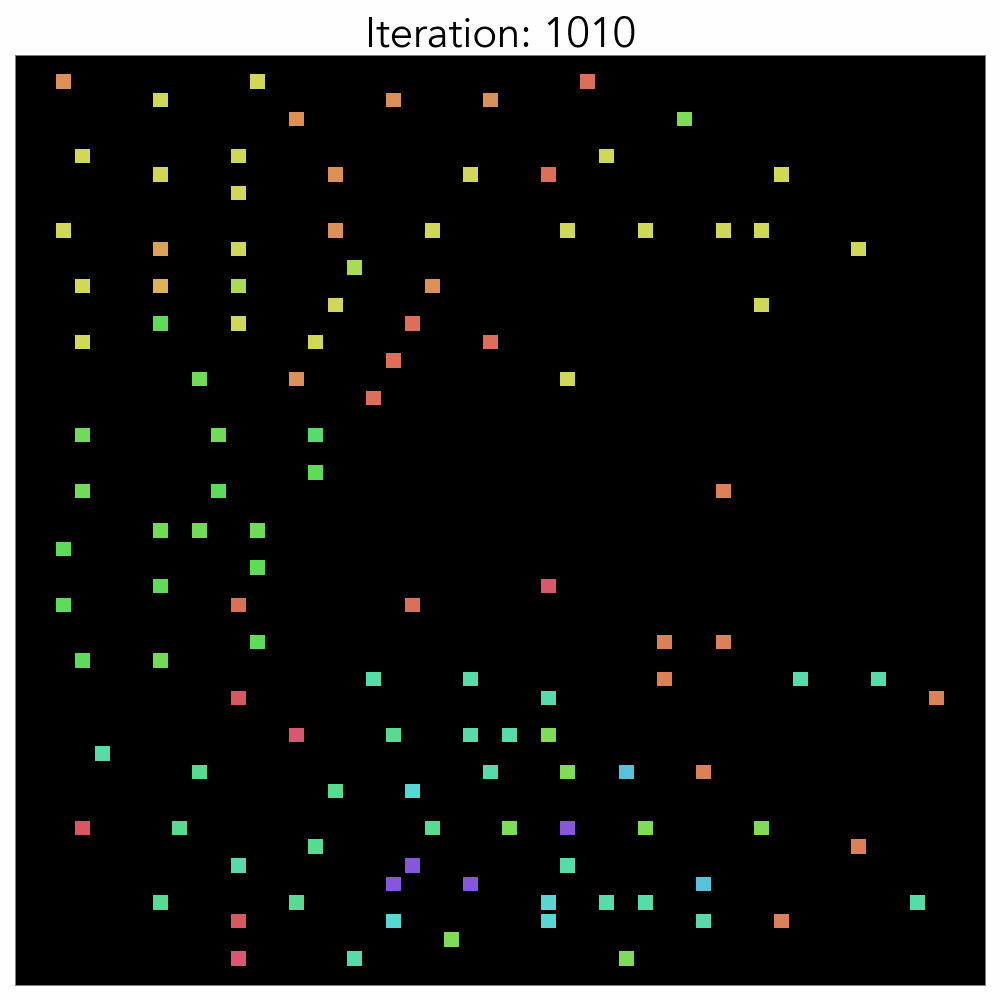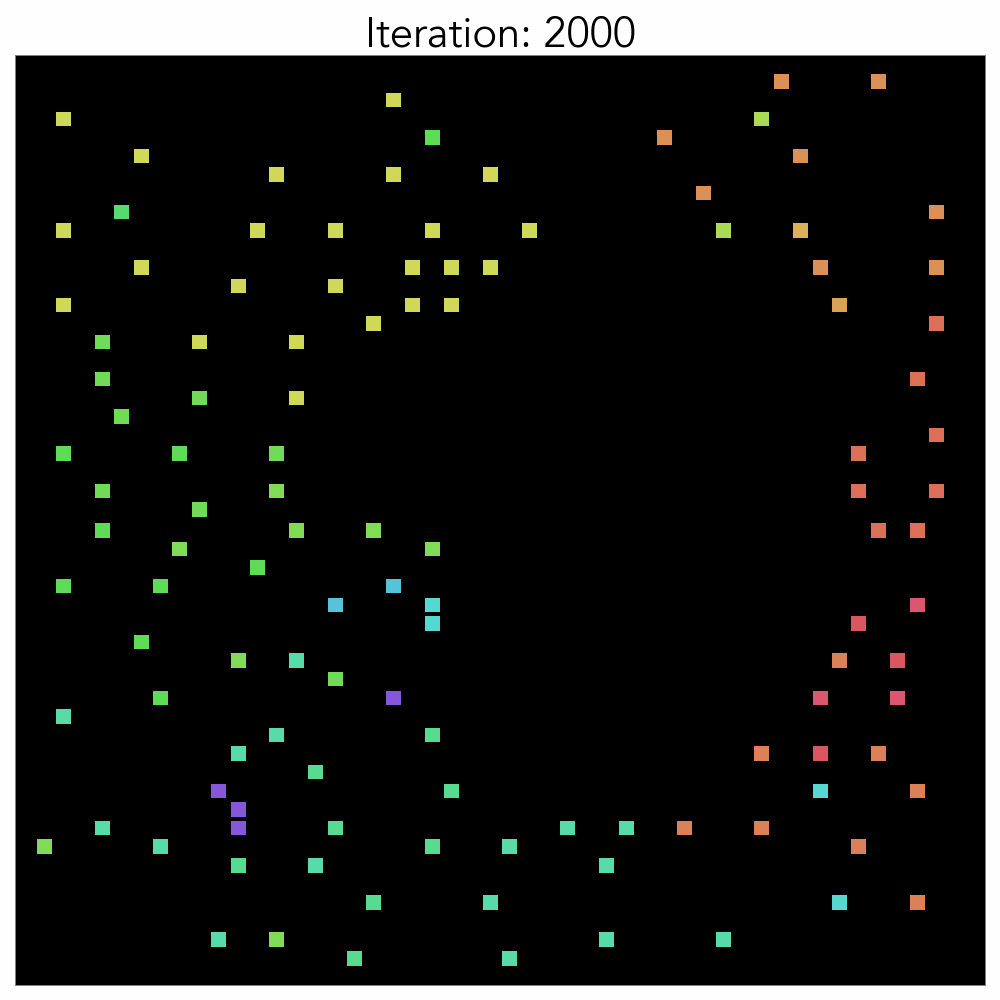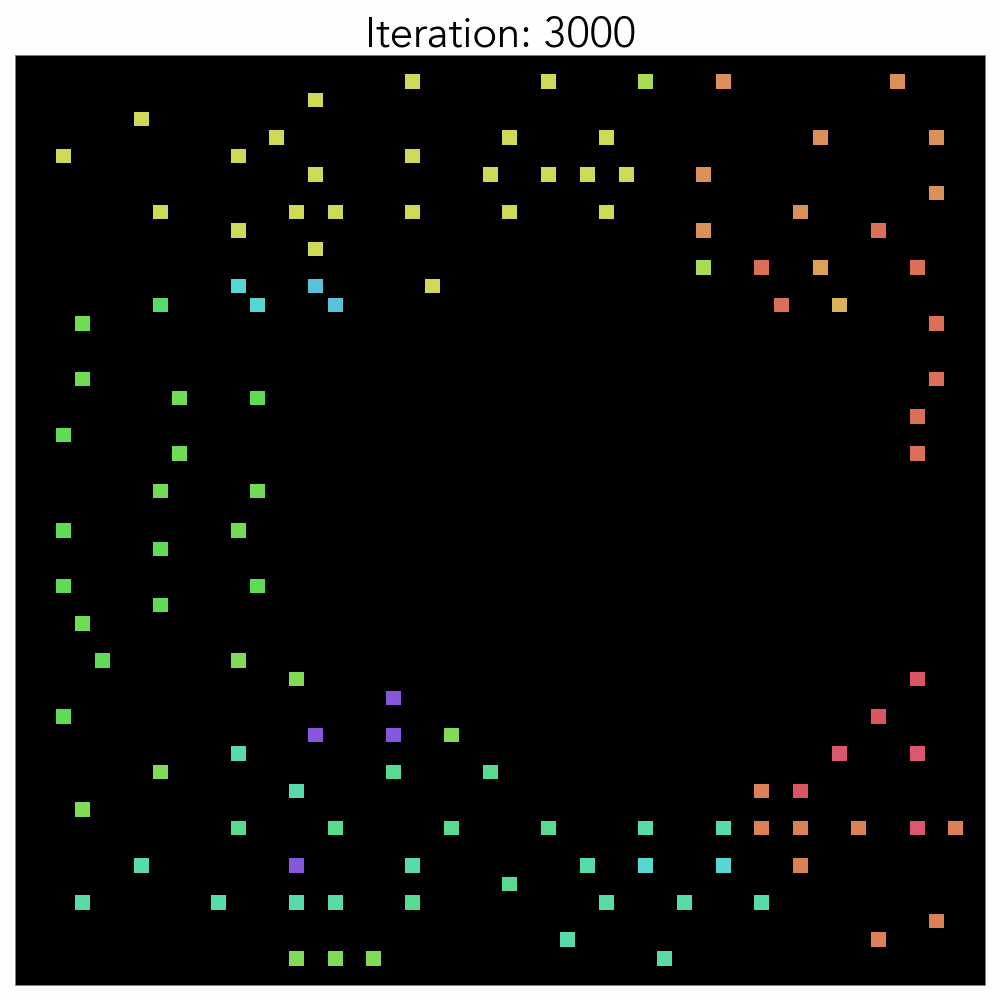
Scenario3: Vanilla RL

마지막 시나리오에서는 별도의 휴리스틱 없이 강화학습만으로 학습했습니다.

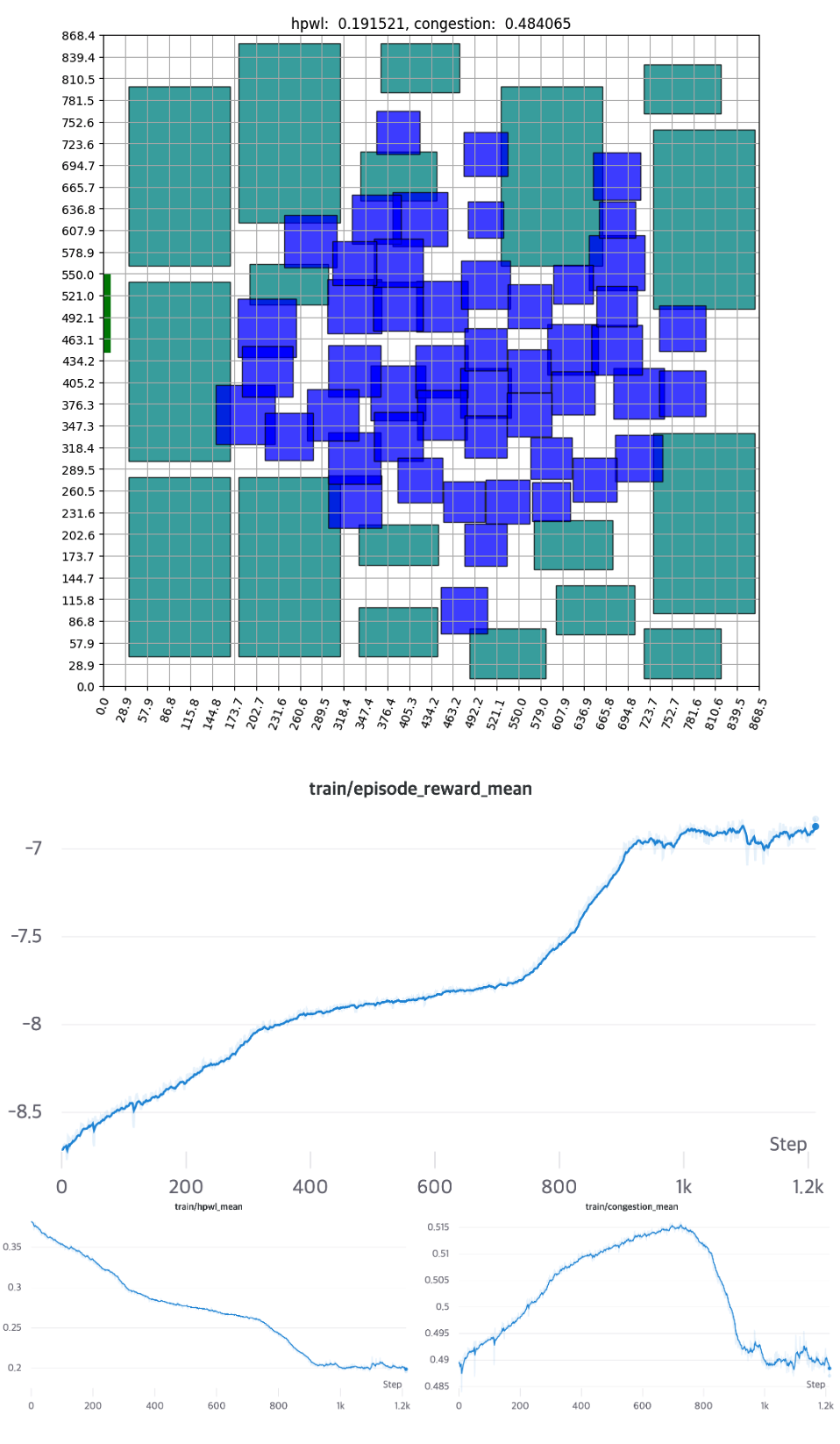
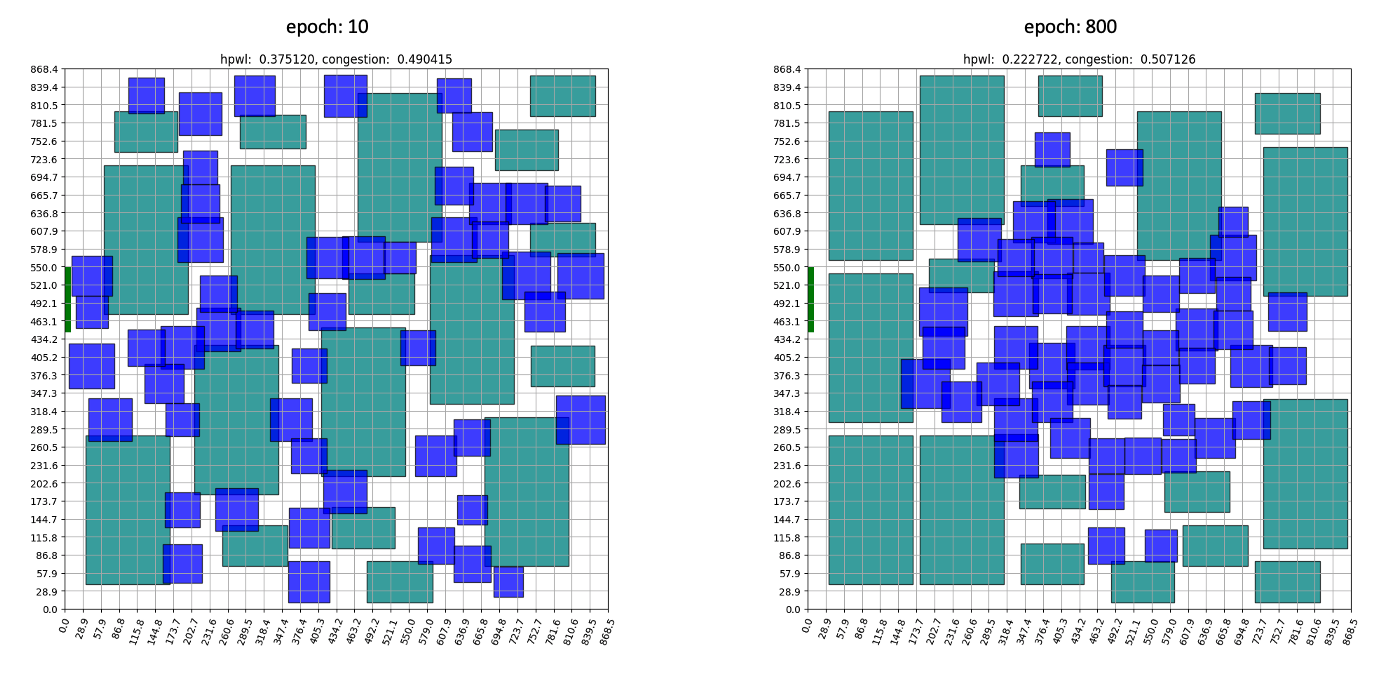
placment at 10 epochs and 800 epochs — [그림 ] - 10 Epochs의 배치 결과와 800 Epochs에서의 배치 결과

학습 초반부에는 무작위로 배치되던 소자들이 중반부로 갈수록 Standard Cell은 중앙으로, Macro는 바깥에 위치하는 모습을 보여줍니다. 이는 전문가의 배치나, Tool을 이용한 Auto Placement와도 상당히 흡사한 모습을 보여줍니다. 학습 그래프를 보면, 직관적인 HPWL을 먼저 줄이고 세밀한 위치 교환을 진행하며 Congestion을 줄입니다. ‘소자들을 가까이 배치’만 하면 되는 HPWL은 직관적인 만큼 학습 초반부터 빠르게 감소하는 모습을 보여줍니다. 반대로, 초반에 Congestion값이 오르는 것으로 보아 학습 초반에는 HPWL이 학습에 더 큰 영향을 미치는걸 알 수 있습니다. 별도의 휴리스틱을 적용하지 않은 경우에는 약 1000 Epochs 후에 수렴합니다.

이 결과가 얼마나 좋은거지?

사실 위의 결과들은 단순히 에이전트의 학습 과정만을 보여줄 뿐, 실제로 어느 정도의 수준인지는 보여주지 않습니다. 학습 결과가 실제로 좋은 건지 확인하기 위해서는 ICC2와 같은 EDA Tool을 사용해 정확한 수치를 측정해야 합니다. 시뮬레이션 결과는 아래 표와 같습니다.

WNS: Worst Negative Slack
FREQ: Frequency

Path Group	Human Experts		ICC2		Single Cluster		Bouding Box		Vanilla RL
Path Group	WNS	FREQ (MHz)	WNS	FREQ (MHz)	WNS	FREQ (MHz)	WNS	FREQ (MHz)	WNS	FREQ (MHz)
Group 0	0.00	143	0.00	143	0.00	143	0.00	143	0.00	143
Group 1	0.05	143	0.06	144	0.14	146	0.05	144	0.07	144
Group 2	0.45	153	0.42	152	0.49	154	0.43	152	0.42	152
Group 3	0.79	161	0.79	161	0.65	158	0.69	158	0.79	160
Group 4	2.60	227	2.65	230	2.66	230	2.60	227	2.55	230
Group 5	2.67	231	2.74	235	2.73	234	2.68	231	2.63	234

Floorplan 단계에서 가장 주의 깊게 봐야 할 수치는 WNS, FREQ 가 있습니다. WNS는 신호가 각 소자에 전달될 때 설계 시 예측했던 시간과 실제 도착시간의 차이를 의미합니다. 만약 0보다 작으면 설계된 조건에 대한 Violation으로 취급되며 Floorplan을 다시 진행해야 합니다. FREQ는 초당 처리한 수 있는 신호의 수, 즉 연산속도를 의미합니다. 그러므로, WNS는 양수인지를 확인하고, FREQ는 값의 크기를 비교합니다. 각 그룹은 성능 검사를 위해 미리 정해둔 Routing Path의 집합입니다. 결과적으로 ‘각 그룹에 대해 WNS가 0 이상이면서 FREQ가 높을 때 성능이 좋다’라고 말할 수 있겠습니다. (각 지표에 대한 자세한 설명은 ASIC-Chip-Placement 1부 포스팅을 참고해주세요.) 결과를 보시면, 저희의 에이전트는 두 가지 Baseline에 근접한 수치를 보여줍니다.

앞으로 풀어야 할 숙제는?

MakinaRocks COP팀에서 개발 중인 강화학습 기반의 알고리즘은 약 12만 개 Standard Cell로 구성된 비교적 작은 규모의 Netlist에 대해서 유의미한 학습 결과를 보였습니다. 이를 기반으로 더 큰 규모의 Netlist에 대한 학습할 예정이며 궁극적으로는 Generalize를 실현해보려 합니다. 목표를 달성하기 위해 앞으로 해결해야 할 문제들이 남아있습니다.

더 적은 시간의 학습으로부터 더 좋은 배치 결과를 얻을 수 있는 방법은?
여러 Netlist에 대해 학습한 후, 보지 못했던 Netlist에 대해 최소한의 학습시간만을 사용해서 좋은 결과를 얻기 위해서는 어떻게 해야 할까?

현재 저희 팀에서는 위에서 언급한 문제들을 해결하기 위해 강화학습에만 국한되지 않고 Simulated Annealing, Genetic algorithm, Force-directed Method 등 여러 최적화 알고리즘의 사용을 같이 고려하고 있습니다. 또한, 앞으로 현업에서 실제 쓰이는 규모인 100만개 단위의 소자 배치도 진행할 예정입니다. 최종적으로는 반도체 Floorplan 문제를 기존 방법론보다 효과적으로 해결할 수 있는 제품을 개발하고자 합니다.

APPENDIX

프로젝트를 진행하면서 여러 가지 Issue들을 Handling하기 위해 적용된 기법들을 소개합니다.

A. Action Design

A.1. Grid Cell Size Decision

행동을 설계할 때는 보상을 최대화할 수 있으면서 가능한 작은 탐색공간이 되도록 설계해야 합니다. 이러한 관점에서 Grid Cell의 크기는 매우 중요합니다. Grid Cell의 크기를 과도하게 작게 하면 충분히 세밀한 탐색이 가능할지는 모르지만, 훈련 시간과 난이도는 Exponential하게 증가할 것입니다. 반대로, Grid Cell을 너무 크게 설정하면 에이전트가 충분히 세밀한 탐색을 할 수 없습니다. 또한, Grid Cell의 크기에 따라서 소자들을 랜덤하게 배치했을 때 공간상의 제약 때문에 모든 소자들을 배치하지 못하는 경우가 빈번하게 발생합니다. 그래서 저희는 특정 범위의 Grid Cell 크기에 대해 각각 $n$번의 배치를 무작위로 진행해 모든 소자를 배치할 확률이 높은 Grid Cell의 크기로 설정했습니다.

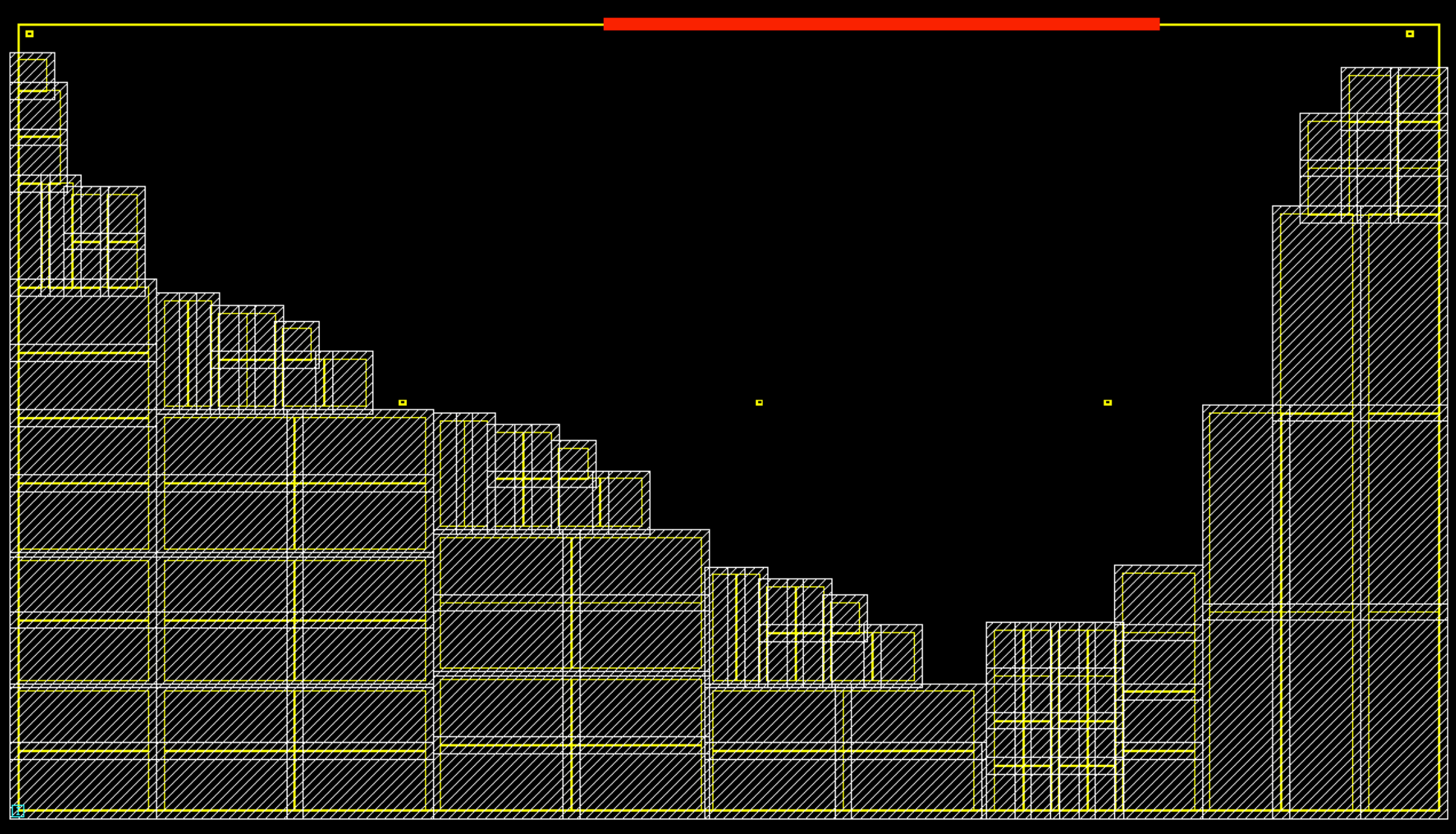
A.2. Invalid Action Masking

현재 배치에 따라 다음 배치될 소자가 배치될 수 있는 영역은 다릅니다. 가장 먼저, 소자 종류와 관계없이 Chip Canvas를 벗어나면 안 됩니다. Macro의 경우에는 다른 소자와 겹침을 허용하면 안 되며, Standard Cell의 경우 배치될 면적과 밀도를 고려해 배치해야 합니다. 이러한 특성들을 고려해 Action을 효과적으로 제어하기 위한 작업이 Invalid Action Masking입니다. 아래 그림은 이 예시를 보여줍니다.

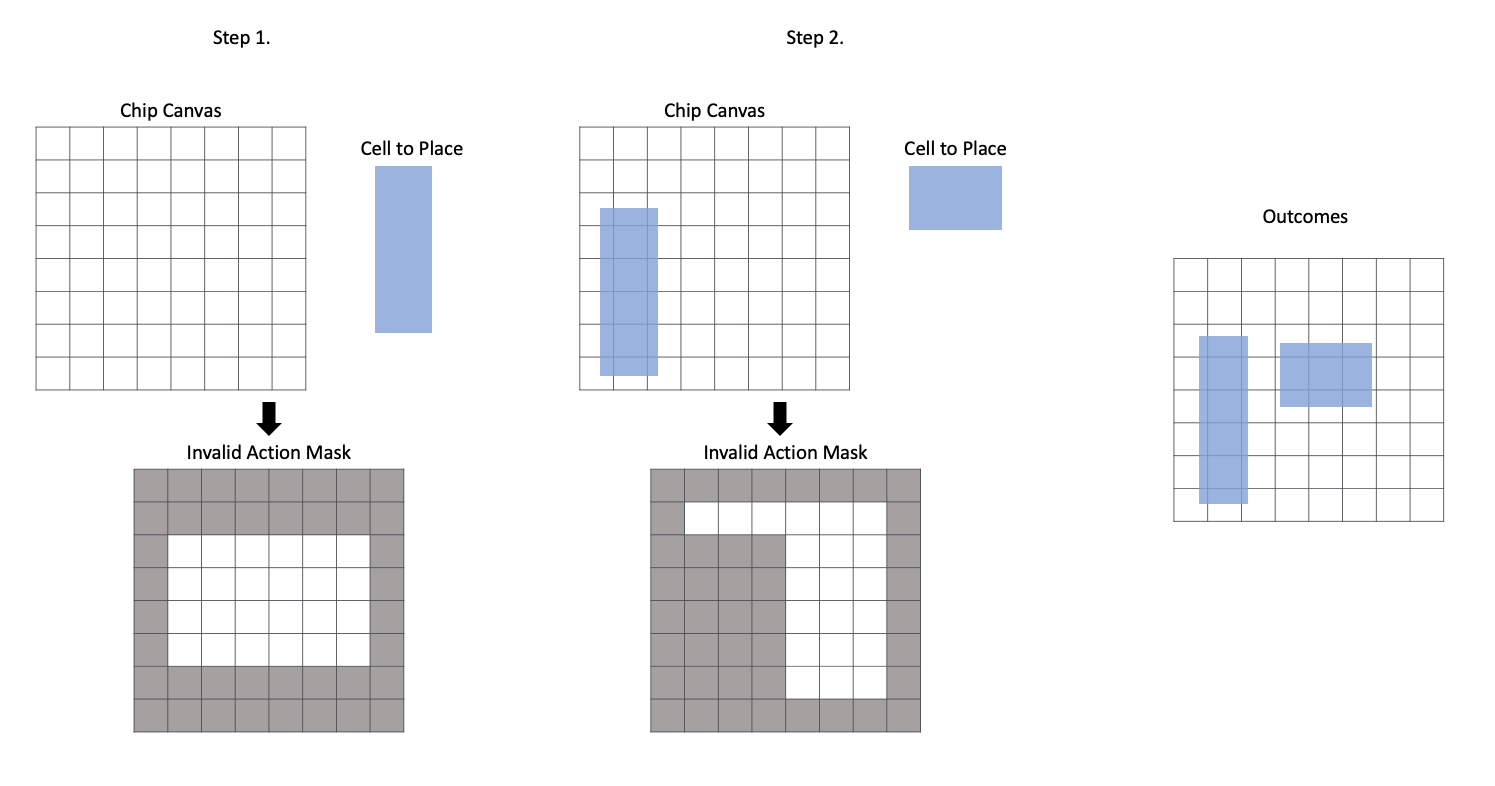
B. Reward Function Design

B.1. Normalization & Reward Coefficient

위에서 설정한 Wire Length와 Congestion을 적절하게 조절하기 위해서는 Normalization과 Coefficient를 활용해야 합니다. 먼저 두 개의 값을 일정 Boundary안에 넣어주기 위해 Normalization을 진행합니다.

Wire Length

HPWL은 Net의 두 소자가 Chip Canvas의 대각선 양 끝단에 위치하는 경우 최댓값을 가집니다. 각 Net에 대해 HPWL을 계산한 뒤 최댓값으로 나누면 효과적으로 [0, 1] 사이의 값으로 바운딩이 가능합니다.

Congestion

Congestion의 경우 Wire Length보다는 약간 더 복잡합니다. Minimum Spanning Tree 혹은 Steiner Tree를 통해 생성된 Edge들이 어떤 Grid Cell을 지날 때, 그 유형은 아래와 같이 4가지가 있습니다.

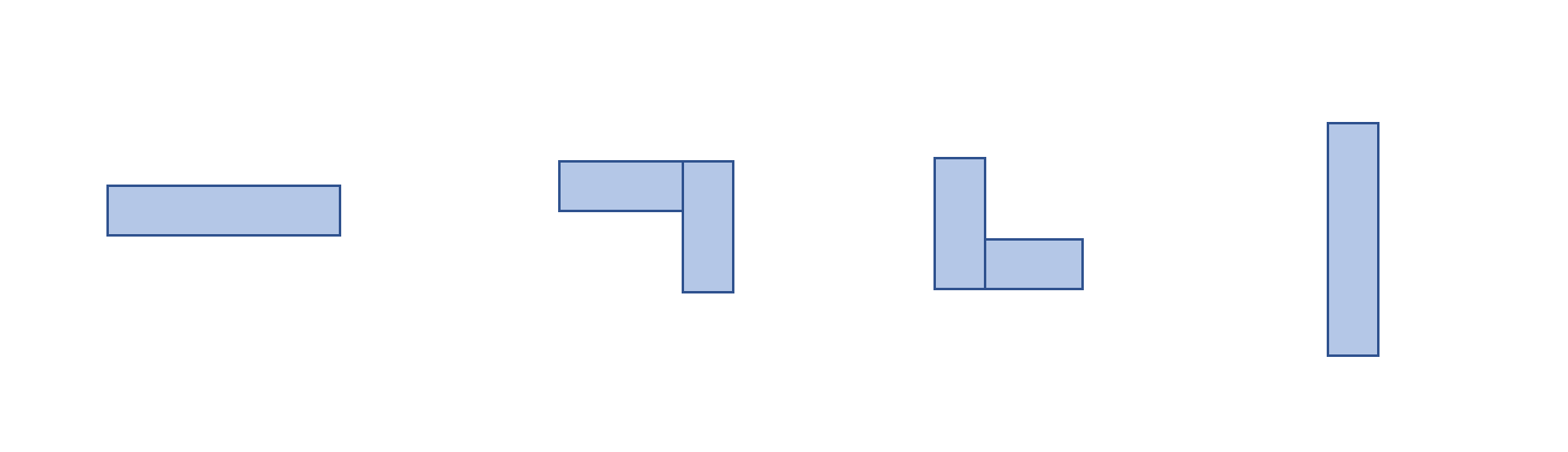
4 paths of edge — [그림 ] - Grid Cell을 지나가는 Edge의 4가지 유형

4가지 유형 모두 Horizontal, Vertical Congestion을 구해 평균값을 취해보면 0.5가 나오는 것을 알 수 있습니다. 즉, 최악의 경우 한 Net의 모든 Edge들이 한 개의 Grid Cell을 지나는 것으로 생각해 볼 수 있을 것입니다. 이 경우의 Congestion 값은 0.5 X n_edges가 되므로 각 Net에 대한 Congestion을 해당 값으로 나누면 역시 [0, 1] 사이의 값으로 바운딩이 가능합니다.

Wire Length와 Congestion에 대해 각각 Normalization 진행 후, Coefficient를 곱해주는 방식으로 둘 사이의 Scaling을 진행합니다.

\[R_{p,g}=-\alpha \cdot WireLength(p,g) - \beta \cdot Congestion(p,g) \qquad \text{S.t. } \text{density}(p,g) \leq \text{max}_\text{density}\]

B.2. Invalid Episode Handling

소자들을 배치하다 보면, 모든 소자들이 배치되기 전 모든 Grid Cell들에 배치 불가능한 상태에 놓이는 경우가 있습니다. Macro는 Overlapping을 아예 허용하지 않다 보니, 큰 Macro 소자가 들어갈 공간이 부족해 생기는 현상입니다. 가장 먼저 소자들을 크기순으로 배치하면 이러한 현상이 발생하는 확률을 줄일 수 있습니다. 하지만, 배치 순서를 정하는 것만으로는 완벽히 해결할 수 없으며, 에이전트에게 배치가 완료되지 않는 상태가 최악의 결과라는 정보를 전달해야 합니다. Invalid Episode가 발생할 경우, 환경은 보상의 하한인 $-\alpha-\beta$ 값을 반환합니다. 에이전트는 보상의 총합을 높이기 위해 Invalid Episode가 발생하지 않는 방향으로 학습합니다.

B.3. Convolution Filter

수십~수백만 개의 Standard Cell에 대한 계산량을 간소화하기 위해 Clustering을 먼저 진행합니다. 이렇게 되면 많은 양의 소자들이 한 개의 Cluster에 묶여 해당 위치의 Congestion 값이 매우 높아지게 됩니다. 이 점을 고려해, 구해진 Congestion Map에 Convolution Filter를 사용해 완화시켜 줍니다.

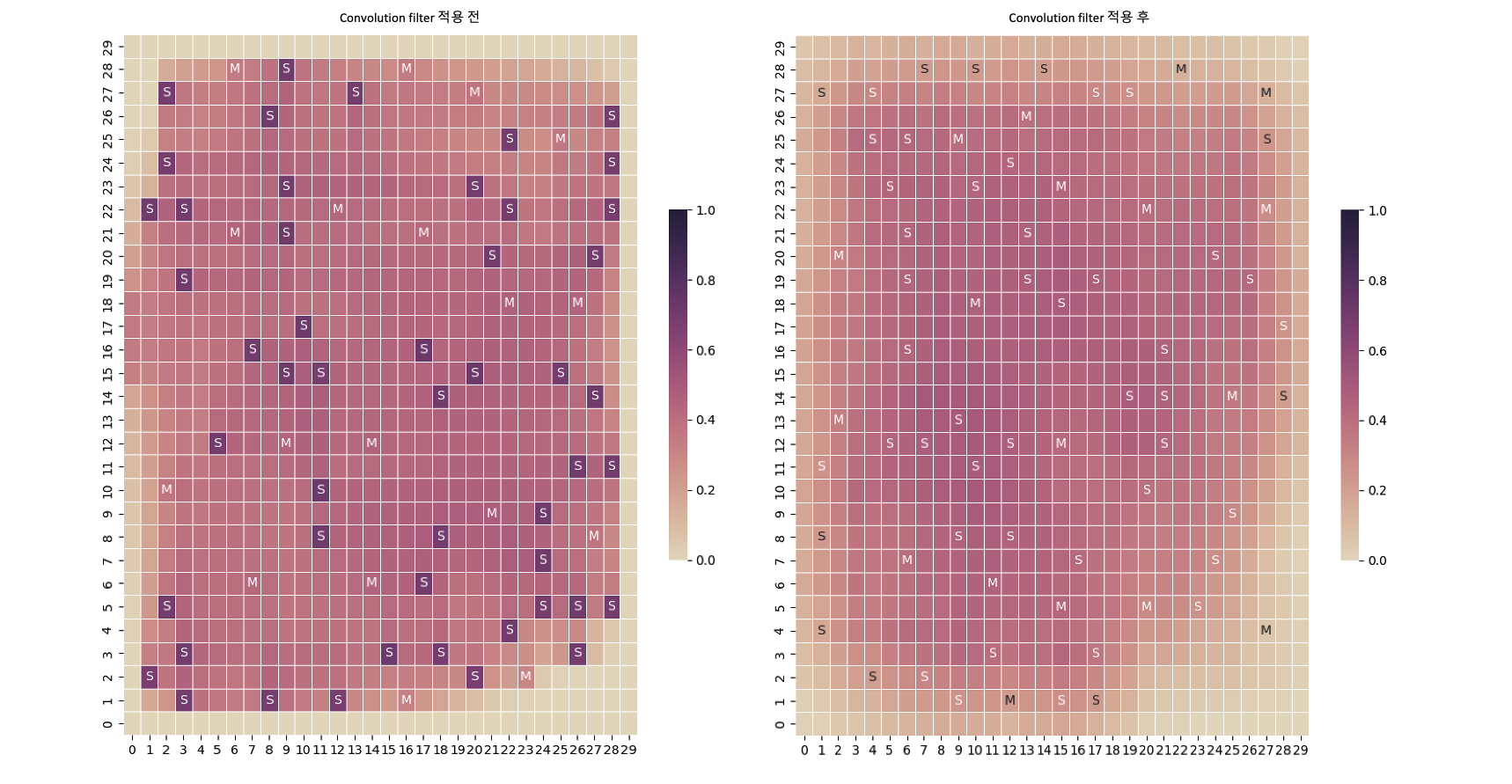
위의 그림을 보시면 Standard Cell Cluster에 과도하게 집중된 Congestion 값(그림에서 S로 표시된 Grid Cell)이 효과적으로 완화된 것을 보실 수 있습니다. 이 작업에 대한 추가적인 이점으로는, Congestion을 주변 영역으로 확장함으로 인해서 Clustering을 진행함으로써 발생한 원본 데이터와의 오차도 줄일 수 있다는 장점도 가지고 있습니다.