Noisy Gradient 다루기

Written by wontak ryu on 29 Dec 2020

들어가며

안녕하세요. 마키나락스의 류원탁입니다.

딥러닝 문제를 다루다보면, Gradient의 오차(Variance)이 커져 학습이 불안정적으로 진행되는 경우가 발생합니다. 여기서 오차라는 표현은 GD에서 나오는 Gradient Vector와 SGD상에서 나오는 Gradient Vector간의 차이를 의미합니다.

본 포스트에서는 Noisy Gradient에 대해서 살펴보고, 해결할 수 있는 방법에 대해서 다루겠습니다.

Noisy Gradient Problem

Stochastic Gradient Descent(SGD)를 활용한 경우, 일반적으로 미니배치의 Gradient는 전체 데이터셋으로부터 구한 Gradient에 비해서 오차(Variance)가 존재할 수 있습니다. 이때 이 Variance가 큰 경우 Gradient가 Noisy하다고 볼 수 있고, 이는 최적화를 수행할 때 어려움으로 작용할 수 있습니다. 이 포스트에서는 이와 같은 문제를 Noisy Gradient Problem이라고 부르도록 하겠습니다.

아래의 이미지들은 Loss Surface에서 Noisy Gradient Problem이 발생하냐에 따른 수렴하는 경향성을 표현한 것들입니다.

SGD를 진행하는 동안, Noisy Gradient Problem이 없다면, [그림1]와 같이 정상적으로 수렴할 수 있습니다.

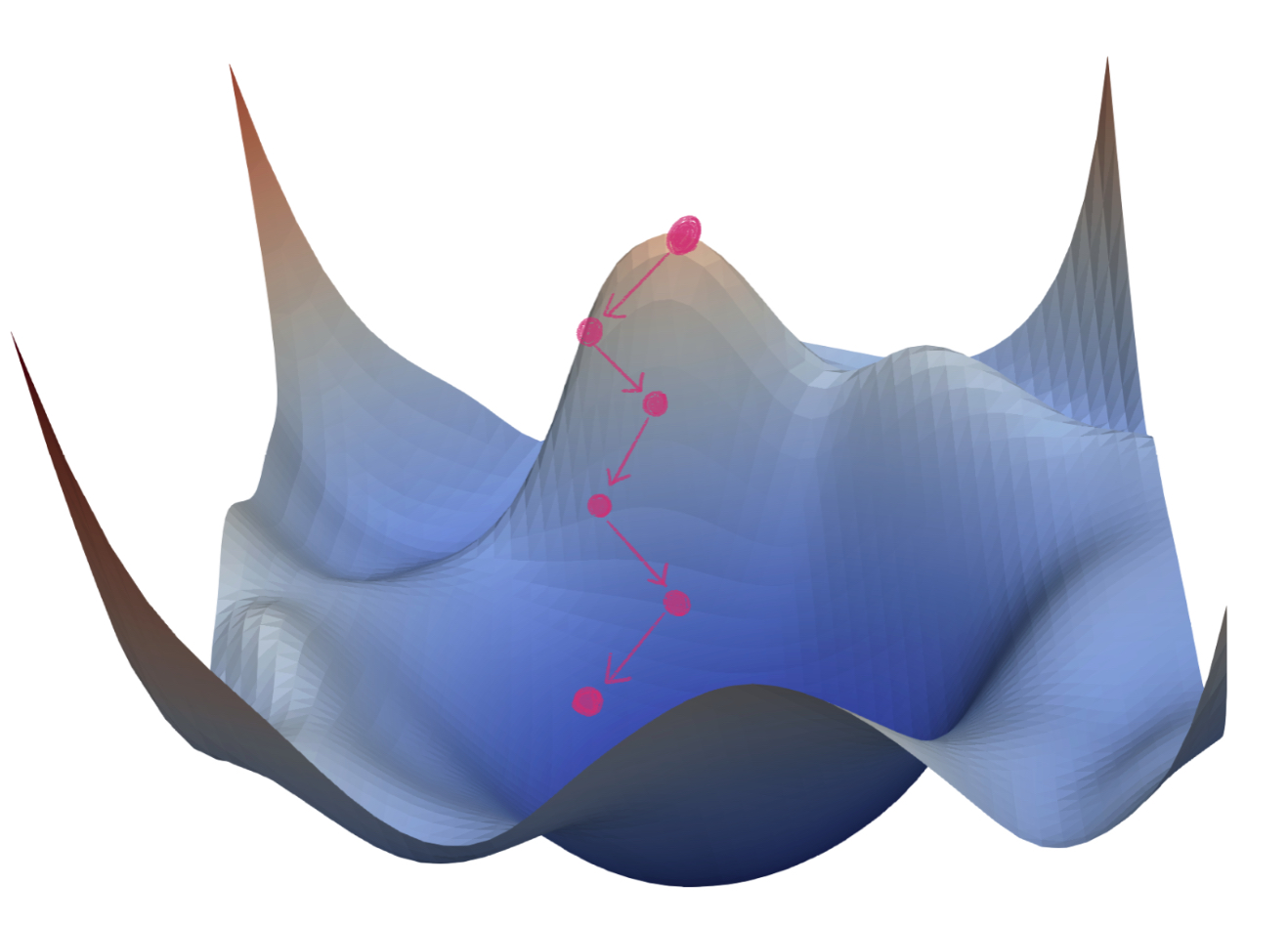
normal gradient — [그림1] - Normal Gradient [16]

반면에, Noisy Gradient Problem을 가지고 있는 모델은 [그림2]와 같이 수렴하는데 어려움을 겪습니다.

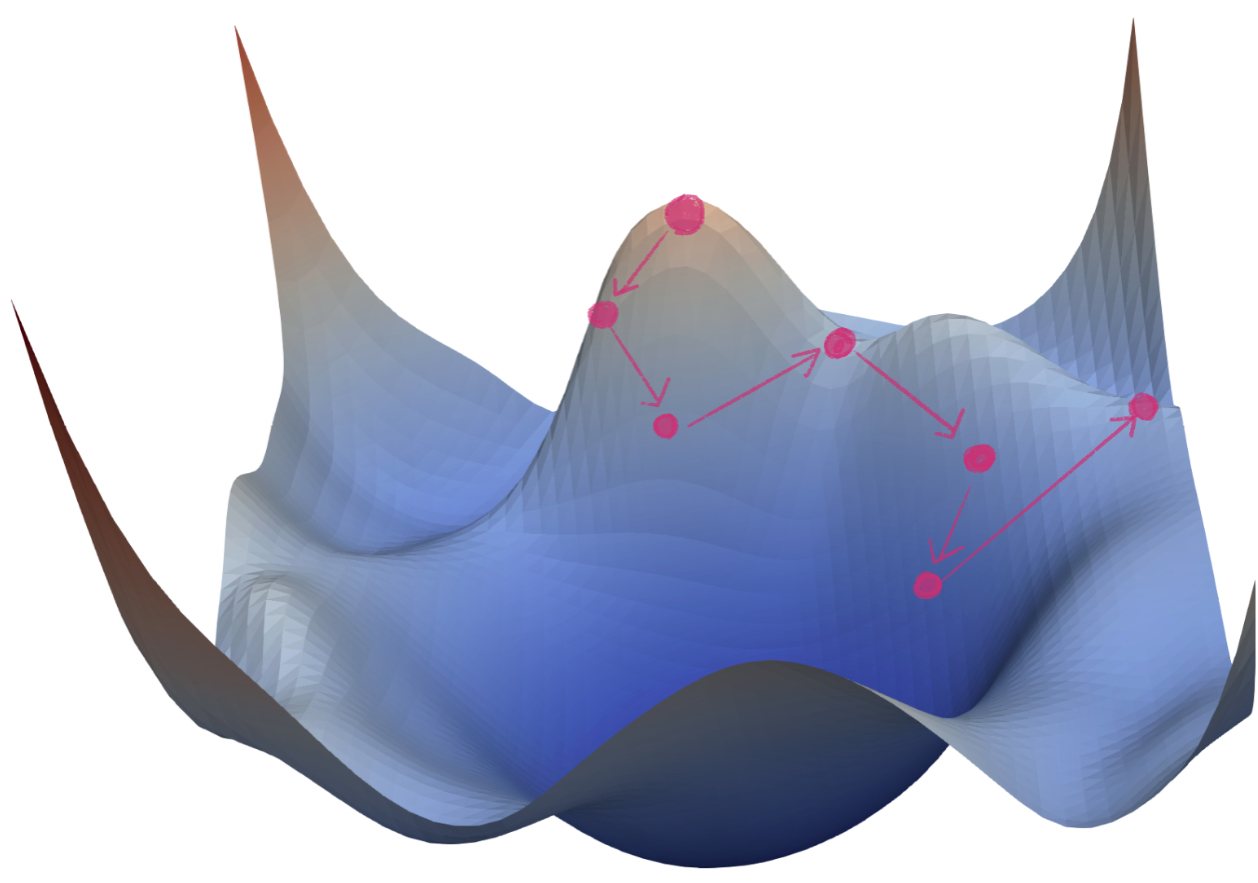
실제로 NLP영역에서 많이 활용되고 있는 Transformer 구조도 이와 같은 문제를 겪었습니다. 실제로 ‘Attention Is All You Need’ 논문을 살펴보면, 학습을 위해서 Warmup을 사용했습니다. Warmup을 사용한 이유는 학습 초기에 발생하는 Noisy Gradient문제를 해결하기 위해서입니다.[3, 6]

이처럼 Noisy Gradient Problem은 원활한 학습을 저해하는 주요한 요인입니다. 다음으로 마키나락스에서 새로운 모델을 개발하면서, 겪은 사례에 대해서 설명드리겠습니다.

사례: Residual AutoEncoder with FC Layer

마키나락스에서도 동일한 문제를 겪었습니다. 마키나락스에서 Anomaly Detection Task를 수행하기 위해서 Autoencoder 구조를 활용하고 있습니다. 다양한 도메인 데이터를 다루고 있는데, 데이터의 특성에 따라서 더 깊은 모델이 요구되기도 합니다. 이 때 단순히 레이어를 더 쌓게되면, Gradient Vanishing의 영향으로 Underfitting 문제가 발생합니다. 이런 문제를 해결하고자 기존에 사용하던 Autoencoder 모델들에 Residual Connection을 추가해봤습니다.

하지만, 예상치 못한 문제가 발생했습니다. 레이어가 깊어질수록 학습이 매우 불안정적으로 진행되었습니다.

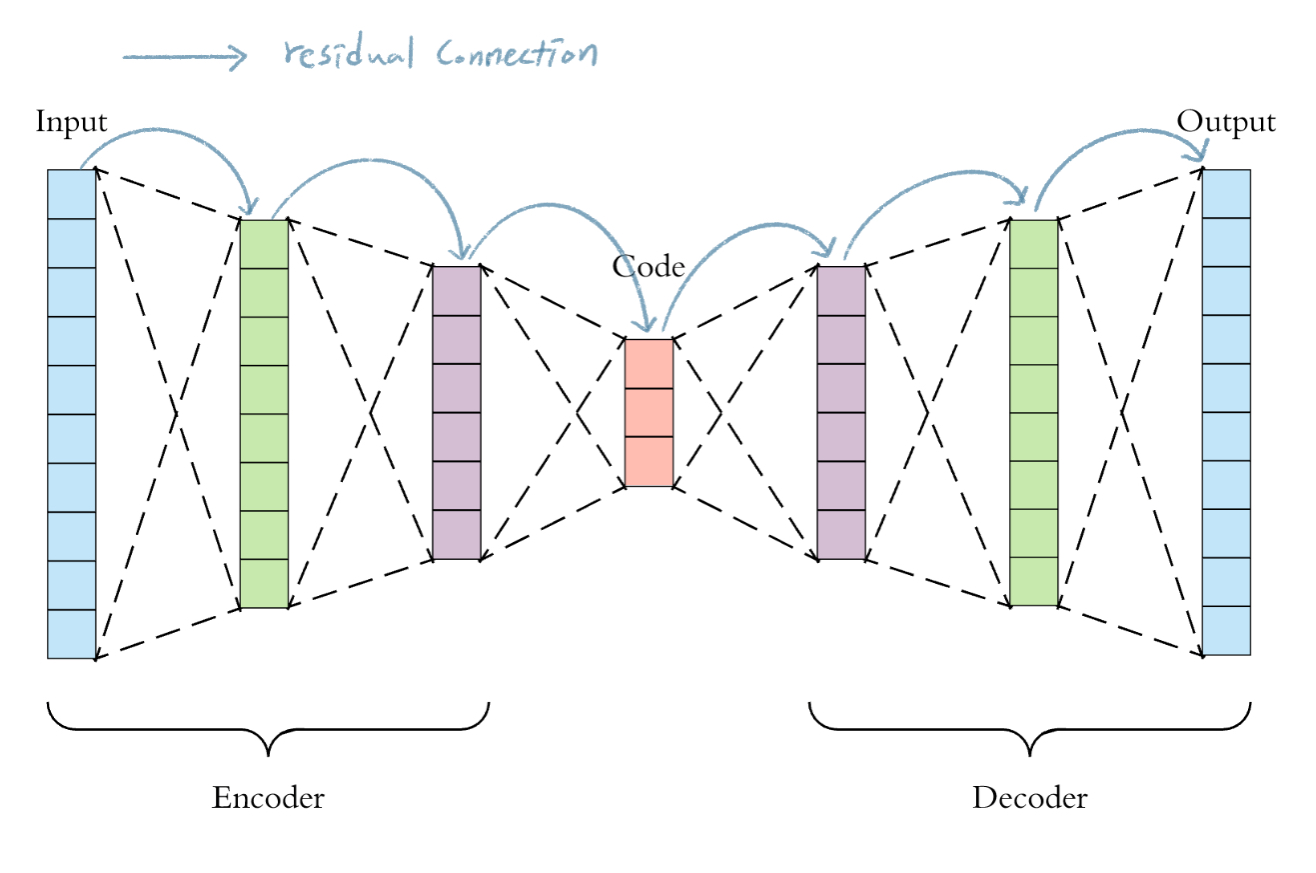
결론적으로 학습에 발생하는 Gradient가 Noisy하다는 문제가 있었습니다. 그렇다면, 기존의 모델과 대비해서 왜 이런 문제가 발생했는지 살펴보겠습니다.

아래와 같이 $\ell$개의 레이어로 이루어진 간단한 모델(No Residual Connection)이 있다고 가정해보겠습니다. 이 모델은 아래와 같은 Forward과정을 가질 것입니다.

$h_i$: i번째 Hidden 레이어의 Output
$f_i$: i번째 Hidden 레이어

\[h_0=x, h_\ell=\hat{y}, \mathbb{loss}=||x-\hat{y}||_2^2\]

Backpropagation은 아래와 같이 전개됩니다.

\[\frac{d \mathbb{loss}}{d h_0} = \frac{d \mathbb{loss}}{d h_{\ell}} \frac{d h_{\ell}}{d h_0} = \frac{d \mathbb{loss}}{d h_{\ell}} \frac{df_{\ell}(h_{\ell - 1})}{dh_0}\]

이제 Residual Connection이 추가된 모델은 어떤 식으로 전개되는지 살펴보겠습니다.

Residual Connection에 대해서 수식으로 표현하면, 아래와 같습니다. [13]

$h_i$: i번째 Hidden 레이어의 Input
$f_i$: i번째 Hidden 레이어

\[h_{i} = f_i(h_{i-1}) + h_{i-1}\]

Forward 과정을 전개해보면, 아래와 같습니다.

$h_i$: i번째 Hidden 레이어의 Output
$f_i$: i번째 Hidden 레이어
$h_0=x$

\[h_\ell=\hat{y} = h_0 + f_1(h_0) + f_2(h_1) + \cdots + f_{\ell}(h_{\ell - 1})\]

이 모델의 Backpropagation과정을 살펴보면 아래와 같습니다.

\[\frac{d \mathbb{loss}}{d h_0} =\frac{d \mathbb{loss}}{d h_{\ell}} \frac{d h_{\ell}}{d h_0} = \frac{d \mathbb{loss}}{d h_{\ell}} \frac{d(h_0 + f_1(h_0) + f_2(h_1) + \cdots + f_{\ell}(h_{\ell - 1}))}{d h_0} \\ =\frac{d \mathbb{loss}}{d h_{\ell}} (1 + \frac{d f_1(h_0)}{dh_0} + \frac{df_2(h_1)}{dh_0} + \cdots + \frac{df_{\ell}(h_{\ell - 1})}{dh_0})\]

간단한 모델(No Residual Connection)과 Residual Connection이 추가된 모델의 Backpropagation 수식을 비교해보면 $\frac{d h_{\ell}}{d h_0}$을 구성하는 부분에서 차이가 있음을 알 수 있습니다. Residual Connection을 추가하게되면, Gradient Vector의 합의 형태로 $\frac{d h_{\ell}}{d h_0}$을 구성하게 됩니다.

각 레이어마다 발생하는 Gradient Vector를 Random Variable로 보면, 위의 Gradient Vector의 Variance은 아래의 식으로 구할 수 있습니다.

우선, 두 Random Variable의 합의 Variance은 아래와 같이 전개됩니다.

\[Var(aX + bY) = a^2 Var(X) + b^2 Var(Y) + 2abCov(XY)\]

이를 위의 Backpropagation의 식에 대입해보면, 기존 모델 대비 더 큰 Variance을 가지는 것을 알 수 있습니다.

$\frac{d f_1(h_0)}{dh_0}, \frac{df_2(h_1)}{dh_0}, \cdots, \frac{df_{\ell}(h_{\ell - 1})}{dh_0}$ 각 요소들이 모두 유사한 스케일을 가진다고 가정해보면, 최소 레이어 수 배 만큼 큰 Variance을 가진다고 할 수 있습니다.

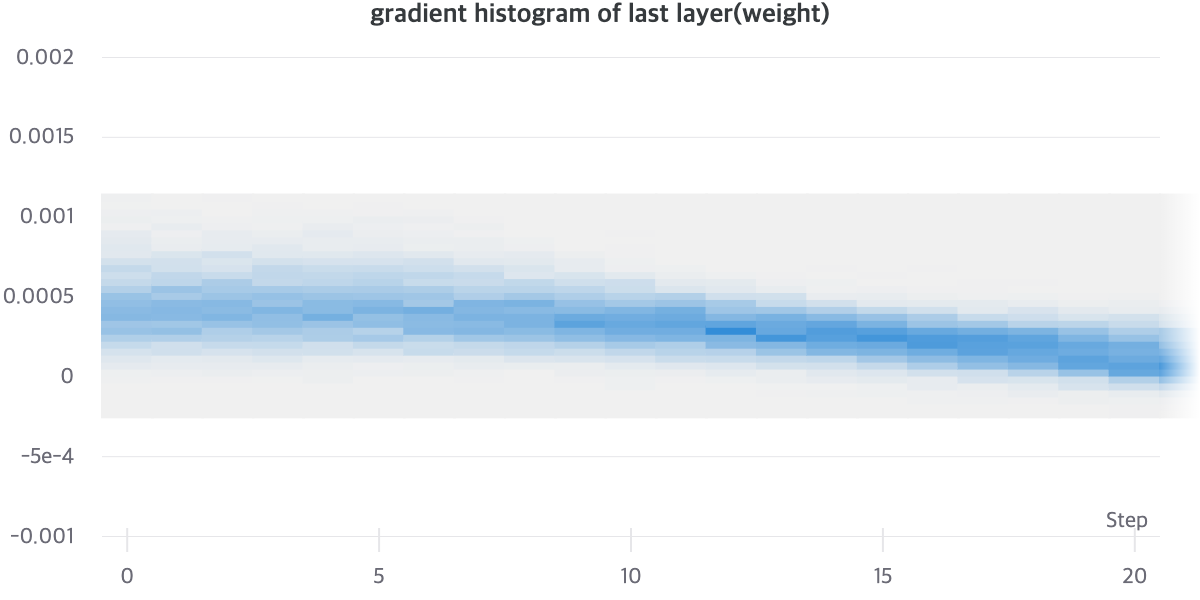
실제로, AutoEncoder와 Residual AutoEncoder의 Gradient Histogram을 살펴보면, 명확한 차이를 알 수 있습니다. AutoEncoder와 Residual AutoEncoder를 비교해보면, Gradient Histogram이 더 Uniform하게 분포해있는 것을 알 수 있습니다. Gradient Histogram이 수렴이 된 모델일 수록 Sharp한 분포를 보이는 것을 고려해보면, Noisy Gradient Problem이 없다면 더 빠르게 Sharp한 Histogram을 가질 것이라고 기대할 수 있습니다. [18]

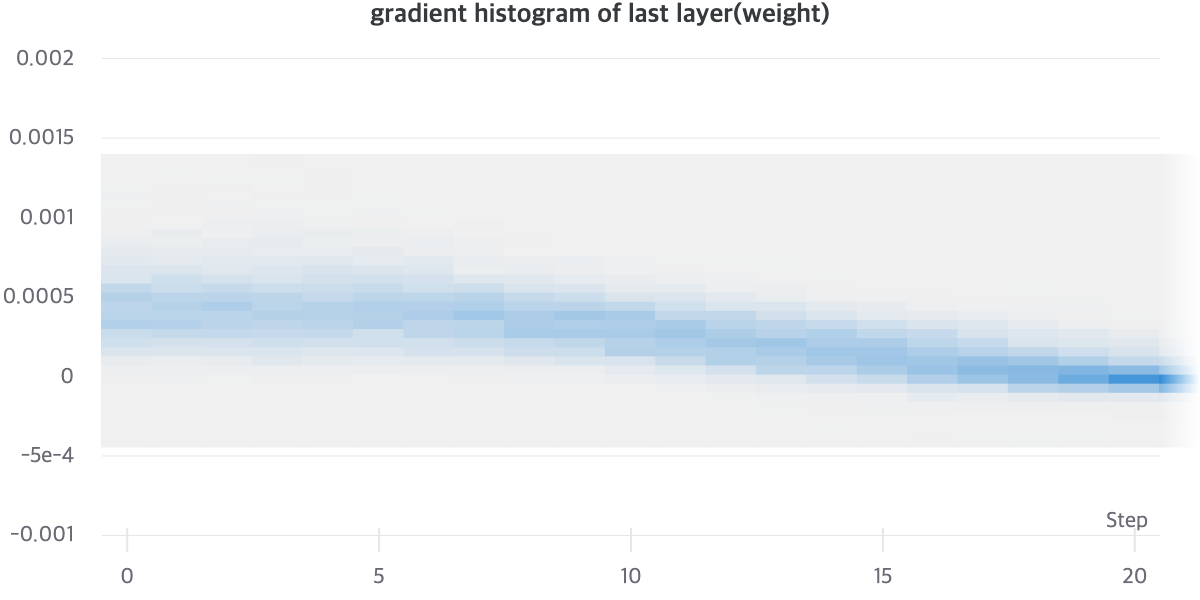
[그래프1], [그래프2]를 통해서 상대적으로 Residual AutoEncoder의 Gradient Vector가 Norm이 더 크게 유지되는 것을 알 수 있으며 Gradient Vector의 분산이 클 것으로 유추할 수 있습니다.

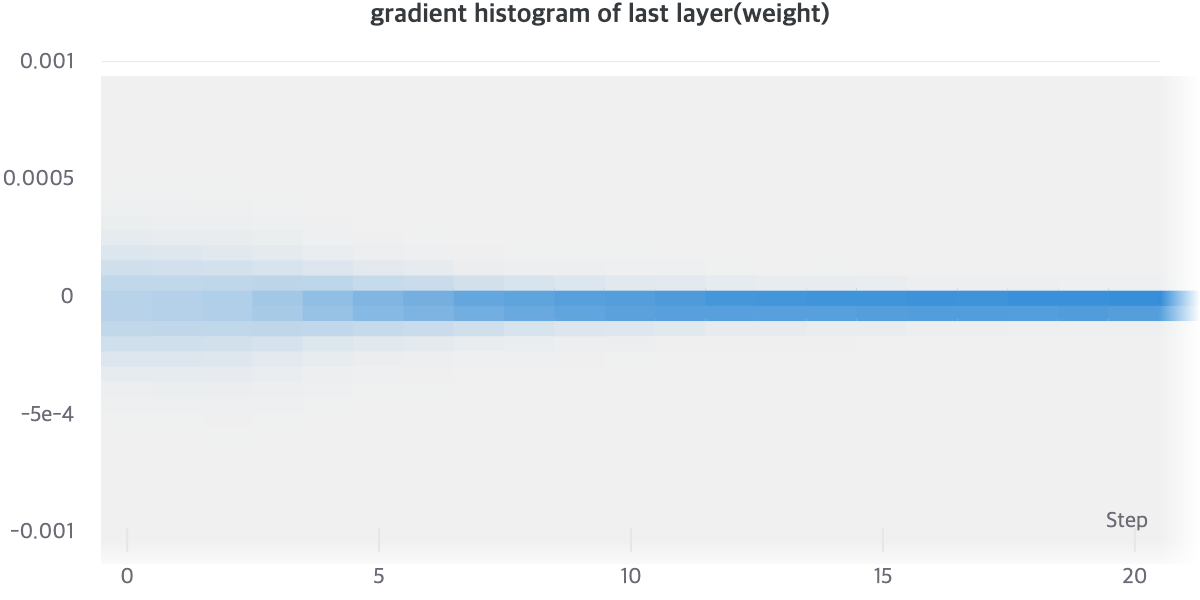
Method: Gradient Accumulation

이런 문제를 해결하기 위해서 아래의 두 가지 방법을 시도를 하였으나, 각각 방법은 명확한 한계를 가지고 있었습니다.

모멘텀을 사용하지 않는 옵티마이저(e.g. AdaGrad, AdaDelta, SGD)를 사용하여 안정적인 학습을 진행했으나, 수렴정도가 만족스럽지 않았습니다.[7, 8, 9]
Warmup을 사용하여 안정적인 학습과 수렴정도도 만족스러웠으나, 하이퍼파라미터에 민감하다는 단점이 있었습니다. [10]

모멘텀을 사용하는 옵티마이저를 활용하면서, 하이퍼파라미터에 상대적으로 덜 민감한 방법에 대해서 고민하기 시작했고, Large Batch Size에서 답을 찾을 수 있었습니다.

Batch Size를 키우게 되면, 통계학적으로 표준편차가 주는 효과가 있습니다. Central Limit Theorem에 따르면 아래와 같은 수식이 전개됩니다. [5]

\[std = \frac{\sigma}{\sqrt{n}}\]

따라서, Batch Size를 키우게되면, 학습이 진행되는 중에 발생하는 Noisy Gradient가 경감되는 것을 알 수 있습니다. 다른 연구에서도 Batch Size가 커지면 학습이 불안정하던 학습이 안정적으로 진행되는 것을 보였습니다. [1, 10]

Batch Size를 키우는 것은 좋지만, Gpu의 Memory는 한정적입니다. 따라서, 한정된 Gpu Memory내에서 Batch Size를 키우는 효과를 내기 위해서, Gradient Accumulation이라는 방법을 사용했습니다. [4, 12]

Gradient Accumulation은 매 Step마다 파라미터를 업데이트 하지않고, Gradient를 모으다가 일정한 수의 Gradient Vector들이 모이면 파라미터를 업데이트합니다.

구체적인 알고리즘을 알고싶다면, 아래의 예시코드를 참고하시기 바랍니다.

model.zero_grad()                                   
for i, (inputs, labels) in enumerate(training_set):
    predictions = model(inputs)                     
    loss = loss_function(predictions, labels)      
    loss = loss / accumulation_steps                
    loss.backward()                                 
    if (i+1) % accumulation_steps == 0:             
        optimizer.step()                            
        model.zero_grad()

모멘텀을 사용하는 옵티마이저의 경우(e.g. Adam, RAdam, RMSprop), 모멘텀을 사용하지 않는 옵티마이저와 비교했을 때 Noisy Gradient에 더 취약합니다. 이는 모멘텀의 구성을 생각해보면, 쉽게 알 수 있습니다. 모멘텀이라는 것은 결국 이전 모멘텀의 정보를 활용하여 현재 모멘텀을 결정하게 됩니다. 이와 같은 작업이 연쇄적으로 동작하게 되고 이는 아래의 수식처럼 표현할 수 있습니다. 결국 모멘텀을 사용하는 옵티마이저의 경우 학습할 때 발생한 Noisy Gradient가 모멘텀 백터에 남게 되고, 이는 수렴을 더욱 방해하는 요인이 됩니다. [14, 15]

$p_0$: 초기 모멘텀 백터
$p_t$: t시점의 모멘텀
$\beta \in (0, 1)$: 모멘텀 팩터
$w_t$: t시점의 weight
$f(w_t)$: $w_t$를 바탕으로 구한 loss

\[p_t = \beta p_{t-1} + \nabla_{w_t} f(w_t) = \sum_{i=0}^{t-1} \beta^{i}\nabla_{w_{t-i}} f(w_{t-i}) + \beta^t p_0\]

이와 더불어, 옵티마이저를 선택할 때도 Noisy Gradient Problem을 고려하여, RAdam을 선택하였습니다. RAdam은 Adam 옵티마이저를 사용시 발생하는 Large Variance of The Adaptive Learning Rates 문제를 해결하기 위해 나온 옵티마이저입니다.[1]

내부실험을 통해서 Adam보다 RAdam이 더 안정적인 학습을 한다는 것을 알 수 있었습니다. 본 포스트에서는 Noisy Gradient와 Gradient Accumulation에 대한 글이므로, 자세히 다루지는 않겠습니다.

Result

Gradient Accumulation을 통해서 불안정적이던 학습을 안정적으로 진행할 수 있었습니다. 또한, Residual VAE를 안정적으로 학습하여 기존의 VAE보다 우수한 성능을 보일 수 있었습니다.

Gradient Accumulation

아래의 [그래프3]은 Residual AutoEncoder를 batch size 6000으로 학습시킨 결과입니다. [그래프2]와 비교해봤을 때, 안정적인 경향성을 보입니다. Step 20을 보면, [그래프2]보다 [그래프3]이 더 모여있는 모습을 볼 수 있습니다.

rae — [그래프3] - RAE Gradient Histogram with batch size 6000

아래의 학습 그래프는 Residual VAE를 기존의 방법대로 학습시킨 것입니다. [그래프4]처럼 학습이 매우 불안정적으로 진행됩니다.

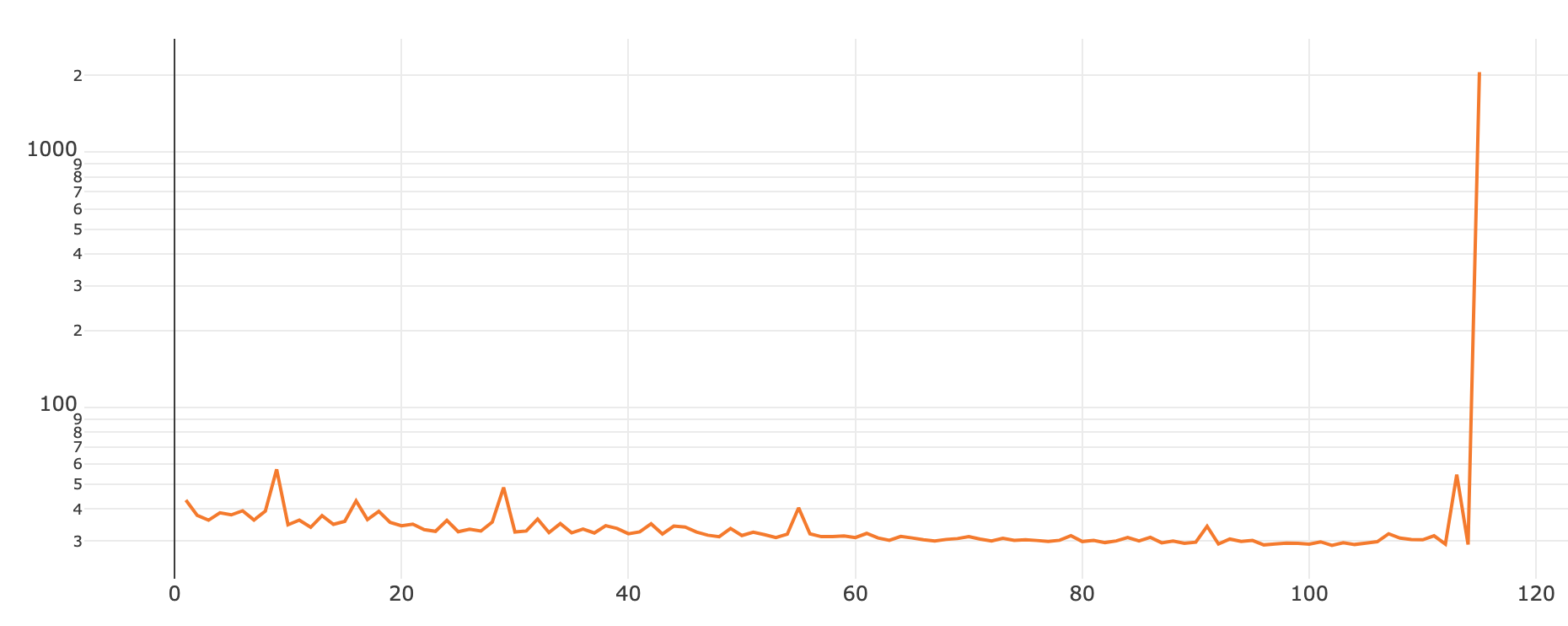
반면에, Gradient Accumulation을 적용하게 되면, [그래프5]처럼 안정적으로 학습이 진행됩니다.

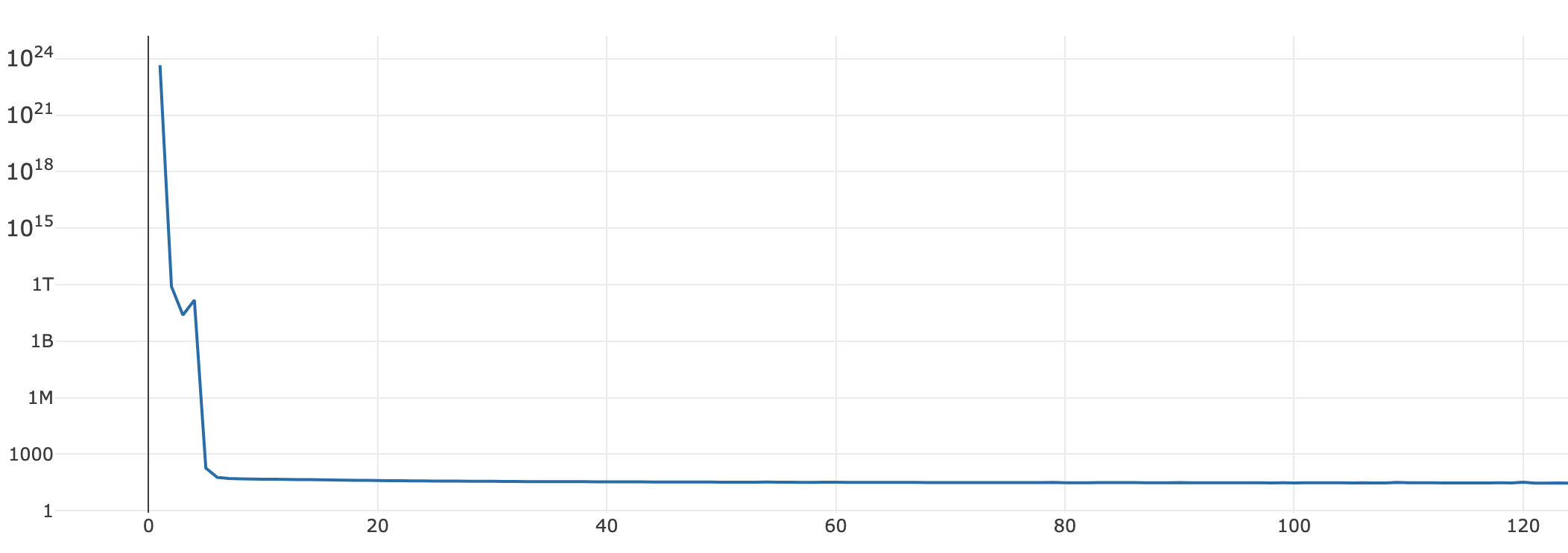
Evaluation: Residual VAE vs. VAE

Residual VAE와 VAE의 실험을 비교해봤습니다.

Anomaly Detection task를 수행하였습니다.
Dataset은 MNIST를 사용했습니다.
실험셋팅은 Class 0, 1을 Target Class를 두고 학습하였으며, 아래의 값은 그것의 평균값입니다.
Target Class 0이라는 것은 0은 비정상 데이터, 나머지 클래스는 모두 정상데이터로 두고 실험하는 셋팅을 의미합니다. 따라서 Train 및 Valid 데이터로 $1, 2, \cdots, 9$ 클래스의 데이터를 활용했으며, Test 데이터로 정상데이터와 비정상데이터를 합쳐서 실험했습니다. 참고로 비정상데이터의 비율은 0.35로 두고 실험하였습니다.
VAE는 Batch Size 256, Residual VAE는 Batch Size 4000으로 두고 실험했습니다.
두 모델 모두 200 Epochs를 학습하였습니다.

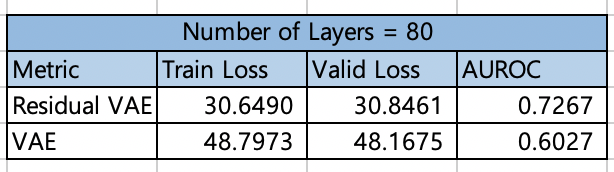
일반적으로 레이어의 수가 80개 정도되면, Gradient Vanishing의 영향으로 학습이 제대로 진행되지 않습니다. 하지만, Residual Connection을 추가해주면, Gradient Vanishing문제가 해결되며 상대적으로 더 낮은 Train Loss와 Valid Loss를 가지는 것을 확인할 수 있으며, Anomaly Detection Task에서도 더 우수한 성능을 보여줍니다.

끝으로

이번 글에서 학습과정에서 발생하는 Noisy Gradient에 대해서 다뤘습니다. 이를 해결하기 위해서 Batch Size를 키우기 위한 노력을 했고, 그 과정에서 발생하는 Gpu Memory 문제를 해결하기 위해서 Gradient Accumulation을 활용했습니다. Gradient Accumulation을 진행하게 되면, Batch Size가 커지는 효과를 가지게 됩니다. [4, 12] Batch Size가 커지게되면, Central Limit Theorem을 통해서 Gradient의 Variance이 줄어드는 효과를 기대할 수 있으며, 이는 안정적인 학습으로 이어질 수 있습니다.[5, 10]

이번 포스트에서는 Noisy Gradient에 대해서 다뤘습니다. 혹시 비슷한 문제를 겪고 있으시다면, 도움이 되었으면 좋겠습니다.